Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có tgy =2/5 = 0,4 ⇒ tgy= tg21048′ ⇒ y= 21048′
x = 900 – 21048′ = 68012′
x – y = 68012′ -21048′ = 46024′
tgy=25=0,4tgy=25=0,4 nên y ≈ 21°48’
Do đó: x = 90° - y ≈ 68°12’
Vậy: x – y ≈ 68°12’ - 21°48’ ≈ 46°24’
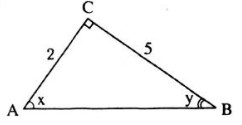

Ta có:
![]()
Suy ra y = 21 ° 48 '
= > x = 90 ° - y = 68 ° 12 ' (x, y là hai góc phụ nhau)
Vậy x – y = 68 ° 12 ' - 21 ° 48 ' = 46 ° 24 '

a: xét (O) có
ΔCAB nội tiếp
AB là đường kính
Do đó: ΔCAB vuông tại C
b: Xét ΔCAB vuông tại C có \(cosBAC=\frac{AC}{AB}=\frac12\)
nên \(\hat{BAC}=60^0\)
ΔACB vuông tại C
=>\(CA^2+CB^2=AB^2\)
=>\(CB^2=AB^2-AC^2=\left(2R\right)^2-R^2=4R^2-R^2=3R^2\)
=>\(CB=R\sqrt3\)
c: Xét (O) có
MC,MB là các tiếp tuyến
Do đó: MC=MB
=>M nằm trên đường trung trực của CB(1)
ta có: OC=OB
=>O nằm trên đường trung trực của CB(2)
Từ (1),(2) suy ra MO là đường trung trực của CB
=>MO⊥CB
mà CA⊥CB
nên CA//OM
d: Gọi I là giao điểm của MA và CH, K là giao điểm của AC và MB
ΔACB vuông tại C
=>CA⊥CB tại C
=>CB⊥AK tại C
=>ΔKCB vuông tại C
Ta có: \(\hat{MCB}+\hat{MCK}=\hat{KCB}=90^0\)
\(\hat{MBC}+\hat{MKC}=90^0\) (ΔKCB vuông tại C)
mà \(\hat{MBC}=\hat{MCB}\) (ΔMBC cân tại M)
nên \(\hat{MCK}=\hat{MKC}\)
=>MC=MK
mà MC=MB
nên MB=MK(3)
ta có: KB⊥BA
CH⊥BA
DO đó: KB//CH
Xét ΔAMK có CI//MK
nên \(\frac{CI}{MK}=\frac{AI}{AM}\left(4\right)\)
Xét ΔAMB có IH//MB
nên \(\frac{IH}{MB}=\frac{AI}{AM}\) (5)
từ (3),(4),(5) suy ra CI=IH
=>I là trung điểm của CH
=>MA đi qua trung điểm I của CH
Ta có:
Suy ra y = 21o48'
=> x = 90o - y = 68o12' (x, y là hai góc phụ nhau)
Vậy x – y = 68o12' - 21o48' = 46o24'