Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tg ABC ( ^A = 90o ) có:
BC2 = AB2 + AC2 (định lý Pytago)
Thay số: BC2 = 3,752 + 4,52
BC2 = 14,0625 + 20,25
BC2 = 34,3125
BC = \(\sqrt{34,3125}\) (BC > 0)
Xét tg ABC có D là đường pg ^A ( gt )
=> \(\dfrac{AB}{AC}=\dfrac{BD}{CD}\)
<=> \(\dfrac{AB}{AC+AB}=\dfrac{BD}{CD+BD}\)
Thay số: \(\dfrac{3,75}{4,5+3,75}=\dfrac{BD}{BC}\)
<=> \(\dfrac{3,75}{8,25}=\dfrac{BD}{\sqrt{34,3125}}\)
=> BD = (cm)
=> CD = BC - CD = (cm)

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=4.5^2+6^2=56.25\)
hay BC=7,5(cm)
Vậy: BC=7,5cm

`Answer:`
Sửa đề câu a.: Tính tỉ số diện tích hai tam giác ABD và tam giác ACD nhé.
C D H A B
a. `\triangleABD` và `\triangleACD` có chung đường cao hạ từ `A`
\(\Rightarrow\frac{S_{ABD}}{S_{ACD}}=\frac{BD}{CD}=\frac{AB}{AC}=\frac{12}{16}=\frac{3}{4}\)
b. Áp dụng định lý Pytago: `AB^2+AC^2=BC^2<=>12^2+16^2=BC^2<=>BC^2=400<=>BC=20cm`
c. Ta có: `BC=BD+CD=20cm`
Mà `\frac{BD}{CD}=3/4=>\frac{BD}{3}=\frac{CD}{4}=\frac{BD+CD}{3+4}=\frac{20}{7}`\(\Rightarrow\hept{\begin{cases}BD=\frac{60}{7}cm\\CD=\frac{80}{7}cm\end{cases}}\)
d. \(S_{ABC}=\frac{1}{2}.AB.AC=\frac{1}{2}.AH.BC\Rightarrow AH=\frac{12.16}{20}=9,6cm\)

a) tg ABD vuong tai A có BD = 2AD (vi góc D=60; C=30)
mà CD=BD ( vì tg CDB cân tại C: có C = B = 30)
VẬY tỷ số AD/CD = BD/CD = 1/2
b) tg ABC = 1/2 TG ĐỀU mà AB=12,5 => BC= 12,5.2 = 25cm
AC = BC\(\sqrt{3}\)/2= 15CĂN3
S= 1/2 . AB.AC = 1/2 , 12,5 . 15căn3 = 93,75\(\sqrt{3}\)cm2
chu vi tg là; 15căn3 + 25+12,5
tôi đã hoàn thành nhiệm vụ, thưa ngài

A là phân giác góc BAC => \(\frac{DC}{DB}\)=\(\frac{AC}{AB}\)=\(\frac{16}{12}\)=\(\frac{4}{3}\)=> \(\frac{DC+DB}{DB}\)=\(\frac{4+3}{3}\)=\(\frac{7}{3}\)
=> \(\frac{BC}{DB}\)=\(\frac{7}{3}\)=> DB= \(\frac{3}{7}BC\)=\(\frac{60}{7}\)cm
=> DC = \(\frac{80}{7}\)cm.
Kẻ DE vuông góc với AC
DE vuông góc với AC và AB vuông góc với AC => DE song song với AB
áp dụng hệ quả của định lý Ta-let,ta có;
\(\frac{DE}{AB}\)=\(\frac{CD}{CB}\)=\(\frac{\frac{80}{7}}{20}\)=\(\frac{4}{7}\)=> DE= \(\frac{4}{7}AB\)=\(\frac{48}{7}\)cm
Diện tích tam giác ACD: S\(_{ACD}\)= \(\frac{1}{2}DE.AC\)=\(\frac{1}{2}.\frac{48}{7}.16\)=\(\frac{384}{7}\)cm\(^2\)
Diện tích tam giác ABD: S\(_{ABD}\)= S\(_{ABC}\)-S\(_{ACD}\)= \(\frac{1}{2}AC.AB\)-\(\frac{384}{7}\)= \(\frac{288}{7}\)cm\(^2\)
Tỷ lệ diện tích tam giác ABD và diện tích tam giác ACD là :\(\frac{3}{4}\)
Độ dài cạnh BC là : BC =\(\sqrt{AB^2+AC^2}\)= 20cm
BD=\(\frac{60}{7}cm\)CD =\(\frac{80}{7}cm\)
Chiều cao AH : S\(_{ABC}\)= \(\frac{1}{2}AC.AB\)=\(\frac{1}{2}AH.BC\)=> AH = \(\frac{AB.AC}{BC}\)=\(\frac{12.16}{20}\)=\(\frac{48}{5}\)cm

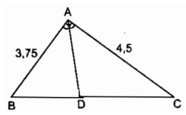
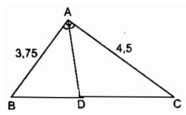

A B D C
Xét \(\Delta ABC\)vuông tại A có :
\(BC^2=AB^2+AC^2\)
\(BC^2=3,75^2+4,5^2\)
\(BC^2=14,0625+20,25\)
\(BC^2=34,875\)
\(\Rightarrow BC=\sqrt{34,875}\)
Xét \(\Delta ABC\)vuông tại A có AD là đường phân giác
\(\Rightarrow\frac{BD}{AB}=\frac{CD}{AC}=\frac{BD+CD}{AB+AC}=\frac{BC}{3,75+4,5}=\frac{\sqrt{34,875}}{8,25}=0,7\)
\(\Rightarrow\frac{BC}{3,75}=\frac{CD}{4,5}=0,7\)
\(\Rightarrow BC=0,7.3,75=2,625\)
\(CD=0,7.4,5=3,15\)