Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Theo hệ quả định lý Ta let ta có:
ΔABC có B’C’ // BC (B’ ∈ AB; C’ ∈ AC) ⇒ 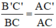
ΔAHC có H’C’ // HC (H’ ∈ AH, C’ ∈ AC) ⇒ 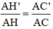
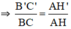
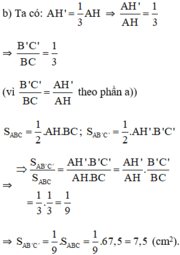

a)
∆ABC có MN // BC.
=> MNCBMNCB = AKAHAKAH(kết quả bài tập 10)
Mà AK = KI = IH
Nên AKAHAKAH = 1313 => MNCBMNCB = 1313 => MN = 1313BC = 1313.15 = 5 cm.
∆ABC có EF // BC => EFBCEFBC = AIAHAIAH = 2323
=> EF = 2323.15 =10 cm.
b) Áp dụng kết quả ở câu b của bài 10 ta có:
bt 10 là bt nào?
vs lại toàn Áp Dụng bài người khác, ko cm?!

a:
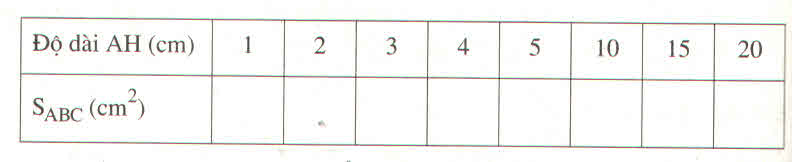
| AH | 1 | 2 | 3 | 4 | 5 | 10 | 15 | 20 |
| S | 2 | 4 | 6 | 8 | 10 | 20 | 30 | 40 |
b: 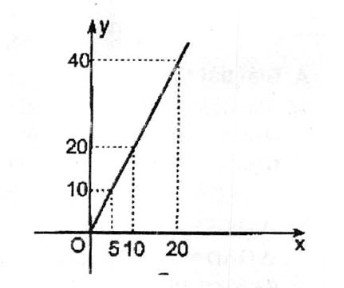
c: Diện tích tam giác tỉ lệ thuận với chiều cao

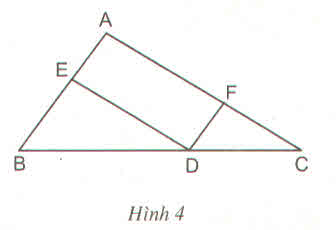
Trong ∆ ABC ta có: DE // AC (gt)
Suy ra: \(\frac{AE}{AB}=\frac{CD}{CB}\)(định lí Ta-lét) (1)
Lại có: DF // AB (gt)
Suy ra: \(\frac{AF}{AC}=\frac{BD}{BC}\)(định lí Ta-lét) (2)
Cộng trừ vế (1) và (2), ta có:
\(\frac{AE}{AB}+\frac{AF}{AC}=\frac{CD}{BC}+\frac{BD}{BC}=\frac{BC}{BC}=1\)

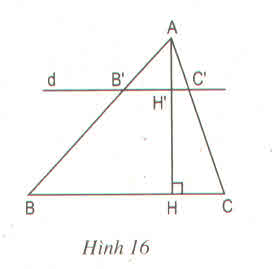
a) Ta có : d // BC
=> B'C' // BC
Xét \(\Delta AB'H'\)và \(\Delta ABH\)( B'H' // BH )
Theo hệ quả của định lý Ta-lét
=> \(\frac{AB'}{AB}=\frac{AH'}{AH}\)(1)
Xét \(\Delta AB'C'\) và \(\Delta ABC\)( B'C' // BC )
Theo hệ quả của định lý Ta-lét
=> \(\frac{AB'}{AB}=\frac{B'C'}{BC}\)(2)
Từ (1) và (2)
=> \(\frac{AH'}{AH}=\frac{B'C'}{BC}\)( ĐPCM )
b) \(\frac{SAB'C'}{SABC}=\frac{\frac{1}{2}AH'.B'C'}{\frac{1}{2}AH.BC}=\frac{AH'}{AH}.\frac{B'C'}{BC}=\frac{1}{3}.\frac{1}{3}=\frac{1}{9}\)
=> \(SAB'C'=\frac{1}{9}\Rightarrow SAB'C'=\frac{SABC}{9}=\frac{67,5}{9}=7,5\left(cm^2\right)\)




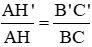 .
.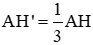 và diện tích tam giác ABC là 67,5 cm
và diện tích tam giác ABC là 67,5 cm
a) Chứng minh AH′AHAH′AH = B′C′BCB′C′BC
Vì B'C' // với BC => B′C′BCB′C′BC = AB′ABAB′AB (1)
Trong ∆ABH có BH' // BH => AH′AHAH′AH = AB′BCAB′BC (2)
Từ 1 và 2 => B′C′BCB′C′BC = AH′AHAH′AH
b) B'C' // BC mà AH ⊥ BC nên AH' ⊥ B'C' hay AH' là đường cao của tam giác AB'C'.
Áp dụng kết quả câu a) ta có: AH' =
a) Chứng minh AH′AHAH′AH = B′C′BCB′C′BC
Vì B'C' // với BC => B′C′BCB′C′BC = AB′ABAB′AB (1)
Trong ∆ABH có BH' // BH => AH′AHAH′AH = AB′BCAB′BC (2)
Từ 1 và 2 => B′C′BCB′C′BC = AH′AHAH′AH
b) B'C' // BC mà AH ⊥ BC nên AH' ⊥ B'C' hay AH' là đường cao của tam giác AB'C'.
Áp dụng kết quả câu a) ta có: AH' = 1313 AH
B′C′BCB′C′BC = AH′AHAH′AH = 1313 => B'C' = 1313 BC
=> SAB’C’= 1212 AH'.B'C' = 1212.1313AH.1313BC
=>SAB’C’= (1212AH.BC)1919
mà SABC= 1212AH.BC = 67,5 cm2
Vậy SAB’C’= 1919.67,5= 7,5 cm2