Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
∆ABC ∽ ∆A'B'C' => = = =
hay = = = =
=> A'B' = 11cm;
B'C' = ≈ 25.67 cm
A'C' = ≈ 18,33 cm
Vì tam giác \(ABC\) đồng dạng với tam giác \(A'B'C'\) nên tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\). Do đó, \(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{{A'B'}}{4} = \frac{{B'C'}}{9} = \frac{{A'C'}}{6}\). Áp dụng tính chất dãy tỉ số bằng nhau ta được:
\(\frac{{A'B'}}{4} = \frac{{B'C'}}{9} = \frac{{A'C'}}{6} = \frac{{A'B' + B'C' + A'C'}}{{4 + 6 + 9}} = \frac{{66,5}}{{19}} = 3,5\)
Ta có:
\(\left\{ \begin{array}{l}\frac{{A'B'}}{4} = 3,5 \Rightarrow A'B' = 3,5.4 = 14\\\frac{{A'C'}}{6} = 3,5 \Rightarrow A'C' = 3,5.6 = 21\\\frac{{B'C'}}{9} = 3,5 \Rightarrow B'C' = 3,5.9 = 31,5\end{array} \right.\)
Vậy \(A'B' = 14cm,A'C' = 21cm,B'C' = 31,5cm\).
Anh mình nghĩ là như thế này. Mà ko biết đúng hay sai .
Ta có : \(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}\)
Suy ra : \(\frac{4,5}{3}=\frac{B'C'}{5}=\frac{C'A'}{7}\)
\(\Rightarrow B'C'=\frac{5.4,5}{3}=7,5\)
\(C'A'=\frac{7.4,5}{3}=10,5\)
Chu vi tam giác A'B'C' là :
4,5 + 7,5 + 10,5 = 22,5 cm
Đ/s : 22,5 cm
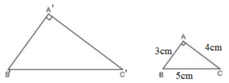
Xét ΔABC có: AB2 + AC2 = 32 + 42 = 25 = 52 = BC2
⇒ ΔABC vuông tại A (Định lý Pytago đảo)
⇒ Diện tích tam giác ABC bằng:
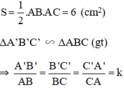
(với k là tỉ số đồng dạng).
Lại có tỉ số diện tích bằng bình phương tỉ số đồng dạng
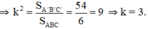
⇒ A’B’ = 3.AB = 3.3 = 9 (cm)
B’C’ = 3.BC = 3.5 = 15 (cm)
C’A’ = 3.CA = 3.4 = 12 (cm)
Vậy độ dài ba cạnh của tam giác lần lượt là 9cm, 12cm, 15cm.
Tam giác A'B'C' đồng dạng với tam giác ABC có cạnh nhỏ nhất bằng 4,5 nên cạnh nhỏ nhất của △ A'B'C' tương ứng với cạnh AB nhỏ nhất của △ ABC
Giả sử A'B' là cạnh nhỏ nhất 'của Δ A'B'C'
Vì
△
A'B'C' đồng dạng
△
ABC nên 
Thay AB = 3(cm), AC = 7(cm), BC = 5(cm), A'B' = 4,5(cm) vào (1) ta có: 
Vậy: 
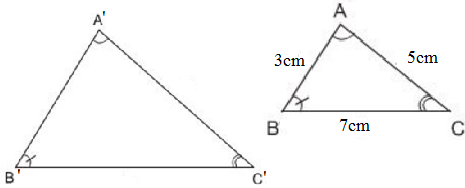
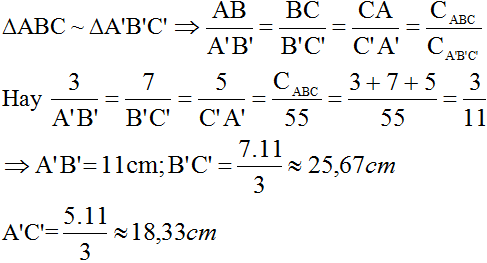
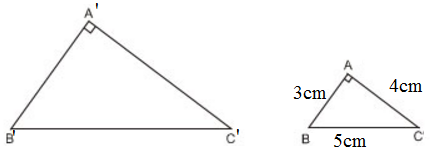
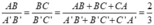
Chu vi tam giác ABC là: AB + BC + CA = 3 + 7 + 5 = 15 (cm)
Δ A’B’C’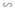
ΔABC ⇒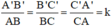 
Áp dụng tính chất dãy tỉ số bằng nhau ta có: