NT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DT
1
NH
1
7 tháng 12 2015
ta có: 6^2+8^2=10^2
=> tam giác ABC vuông
Sabc=(6.8):2=48:2=24(cm)
4 tháng 3 2022
a: BC=10cm
b: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\)
Do đó: ΔHAB∼ΔHCA
11 tháng 1 2022
1: \(S=\dfrac{AB\cdot AC}{2}=24\left(cm^2\right)\)
2: \(S=\dfrac{5\cdot8}{2}=20\left(cm^2\right)\)
3: Số viên gạch cần dùng là:
\(400\cdot600:33.33^2\simeq217\left(viên\right)\)
8 tháng 1 2022
a) \(\Delta ABC\) vuông tại A (gt).
\(\Rightarrow S_{\Delta ABC}=\dfrac{1}{2}AB.AC=\dfrac{1}{2}6.8=24\left(cm^2\right).\)
b) Xét \(\Delta ABC\) vuông tại A:
\(BC^2=AB^2+AC^2.\Rightarrow BC^2=6^2+8^2.\Leftrightarrow BC^2=36+64=100.\)
\(\Rightarrow BC=10\left(cm\right).\)
c) Ta có: \(S_{\Delta ABC}=\dfrac{1}{2}AH.BC.\)
\(S_{\Delta ABC}=\dfrac{1}{2}AB.AC.\)
\(\Rightarrow\dfrac{1}{2}AH.BC=\dfrac{1}{2}AB.AC.\)
\(\Rightarrow\dfrac{1}{2}AH.10=24.\Leftrightarrow AH=4,8\left(cm\right).\)
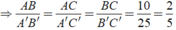
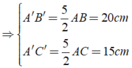
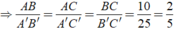
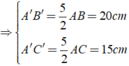
Tam giác trên có 3 cạnh 6,8,10 là bộ ba Py-ta-go => Đây là tam giác vuông có cạnh huyền =10
=> S= \(\frac{6.8}{2}\)=24(cm\(^2\))