Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

nhanh lên mình cần gấp lắm
giúp mình với huhuhuhuhuhuhuhuhuhuhuhuhuhuhuhuhuhu

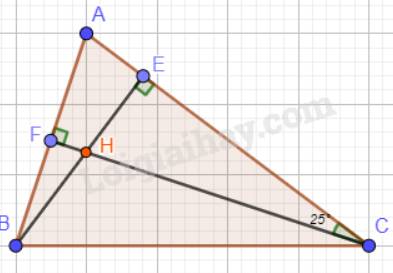
Xét tam giác AFC có: \(\widehat {HCA} = 25^\circ \); \(\widehat {AFC} = 90^\circ \) (vì CF vuông góc với AB).
Nên: \(\widehat {FAC} = \widehat {BAC} = 90^\circ - 25^\circ = 65^\circ \).
Xét tam giác AEB có: \(\widehat {BAC} = 65^\circ \); \(\widehat {AEB} = 90^\circ \)(vì BE vuông góc với AC).
Nên: \(\widehat {ABE} = \widehat {HBA} = 90^\circ - 65^\circ = 25^\circ \).

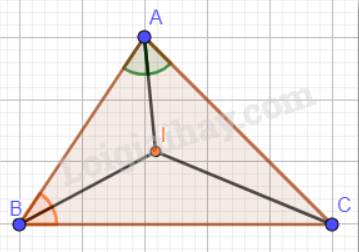
Ta có: I là giao điểm của hai đường phân giác góc A và góc B nên suy ra: CI là đường phân giác của góc C.
Vậy \(\widehat {ICA} = \widehat {ICB}\) ( tính chất tia phân giác của một góc).
Đáp án: A. \(\widehat {ICA} = \widehat {ICB}\).

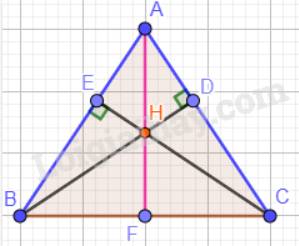
a) Tam giác ABC cân tại A nên: \(\widehat {ABC} = \widehat {ACB} = 70^\circ \).
Tổng ba góc trong một tam giác bằng 180° nên: \(\widehat {BAC} = 180^\circ - 70^\circ - 70^\circ = 40^\circ \).
b) Xét tam giác vuông ADB và tam giác vuông AEC có:
AB = AC (tam giác ABC cân);
\(\widehat A\) chung.
Vậy \(\Delta ADB = \Delta AEC\)(cạnh huyền – góc nhọn). Suy ra: BD = CE ( 2 cạnh tương ứng).
c) Trong tam giác ABC có H là giao điểm của hai đường cao BD và CE nên H là trực tâm trong tam giác ABC hay AF vuông góc với BC.
Xét hai tam giác vuông AFB và AFC có:
AB = AC (tam giác ABC cân);
AF chung.
Vậy \(\Delta AFB = \Delta AFC\)(cạnh huyền – cạnh góc vuông). Suy ra: \(\widehat {FAB} = \widehat {FAC}\) ( 2 góc tương ứng) hay \(\widehat {BAH} = \widehat {CAH}\).
Vậy tia AH là tia phân giác của góc BAC.

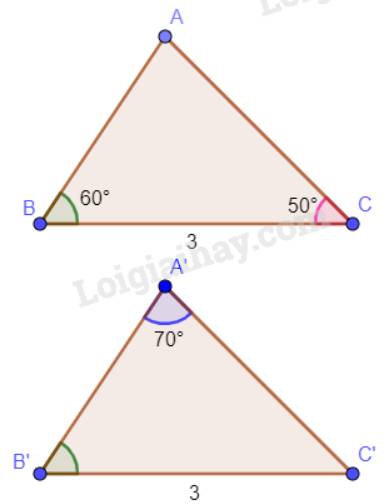
Tổng ba góc trong một tam giác bằng 180°. Vậy trong tam giác A’B’C’ có \(\widehat {C'} = 180^\circ - 70^\circ - 60^\circ = 50^\circ \).
Xét hai tam giác ABC và A’B’C’ có:
\(\widehat B = \widehat {B'} = 60^\circ ;\)
BC = B’C’ ( = 3 cm)
\(\widehat C = \widehat {C'} = 50^\circ \)
Vậy \(\Delta ABC = \Delta A'B'C'\)(g.c.g)

a) I là giao điểm của ba đường phân giác tại ba góc A, B, C nên:
\(\widehat {IAB} = \widehat {IAC};\widehat {IBA} = \widehat {IBC};\widehat {ICB} = \widehat {ICA}\).
Tổng ba góc trong một tam giác bằng 180° nên:
\(\begin{array}{l}\widehat {BAC} + \widehat {ACB} + \widehat {CBA} = 180^\circ \\\widehat {IAB} + \widehat {IAC} + \widehat {IBA} + \widehat {IBC} + \widehat {ICB} + \widehat {ICA} = 180^\circ \\2\widehat {IAB} + 2\widehat {IBC} + 2\widehat {ICA} = 180^\circ \end{array}\)
Vậy \(\widehat {IAB} + \widehat {IBC} + \widehat {ICA} = 90^\circ \).
b) Tổng ba góc trong một tam giác bằng 180°. Xét tam giác BIC:
\(\begin{array}{l}\widehat {BIC} + \widehat {IBC} + \widehat {ICB} = 180^\circ \\\widehat {BIC} = 180^\circ - (\widehat {IBC} + \widehat {ICB})\end{array}\).
Mà \(\widehat {IAB} + \widehat {IBC} + \widehat {ICA} = 90^\circ \)→ \(\widehat {IBC} + \widehat {ICA} = 90^\circ - \widehat {IAB}\).
Vậy: \(\begin{array}{l}\widehat {BIC} = 180^\circ - (\widehat {IBC} + \widehat {ICB})\\\widehat {BIC} = 180^\circ - (90^\circ - \widehat {IAB})\\\widehat {BIC} = 90^\circ + \widehat {IAB}\end{array}\)
Mà \(\widehat {IAB} = \dfrac{1}{2}\widehat {BAC}\)(IA là phân giác của góc BAC).
Vậy \(\widehat {BIC} = 90^\circ + \widehat {IAB} = 90^\circ + \dfrac{1}{2}\widehat {BAC}\).