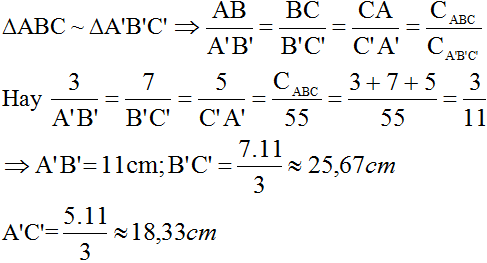Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D
Độ dài cạnh AB,BC :
66 : 2 = 33 (cm)
vậy cạnh AC dài là :
56 - 33 = 23 (cm)
vậy cạnh AC dài 23 (cm)
mọi người cho mih xin 1 cái k nha

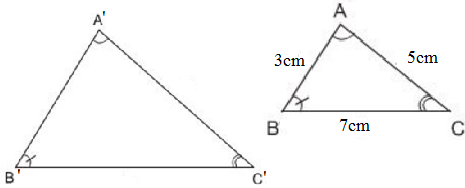
Chu vi tam giác ABC là 3 + 5 +7 = 15
Ta có :
P ABC / P A'B'C' = AB / A'B'
<=> 15 / 55 = 3 / A'B'
=> A'B' = ( 55 x 3 )/ 15 = 11 cm
P ABC / P A'B'C' = AC / A'C'
<=> 15 / 55 = 5 / A'C'
=> A'C' = ( 55 x 5 ) / 15 = 55/3 cm
P ABC / P A'B'C' = BC / B'C'
<=> 15 / 55 = 7 / B'C'
=> B'C' = ( 55 x 7 ) / 15 = 77/3 cm
A B C A' B' C'
\(\Rightarrow\Delta ABC\)đồng dạng \(\Delta A'B'C'\left(gt\right)\)
Áp dụng tính chất DTSBN , ta có :
\(\frac{AB}{A'B'}=\frac{AC}{A'C'}=\frac{BC}{B'C'}=\frac{AB+AC+BC}{A'B'+A'C'+B'C'}=\frac{C_{ABC}}{C_{A'B'C'}}\)
Hay \(\frac{3}{A'B'}=\frac{7}{B'C'}=\frac{5}{A'C'}=\frac{C_{ABC}}{55}=\frac{3+5+7}{55}=\frac{15}{55}=\frac{3}{11}\)
Với CABC và CA'B'C' lần lượt là chu vi của tam giác ABC , A'B'C'
\(+)\frac{3}{A'B'}=\frac{3}{11}\Rightarrow A'B'=\frac{3.11}{3}=11cm\)
\(+)\frac{7}{A'C'}=\frac{3}{11}\Rightarrow B'C'=\frac{7.11}{3}\approx25,67cm\)
\(+)\frac{5}{A'C'}=\frac{3}{11}\Rightarrow A'C'=\frac{5.11}{3}\approx18,33cm\)

chu vi tam giác ABC + chu vi tam giác ACD - chu vi tứ giác ABCD = 2AC
hay 56 + 60 - 66 = 2AC
Vậy AC = 25 (cm)

Bài 1: Có P(ABCD) = AB + BC + CD + DA = 66
P(ABC) = AB + BC + CA = 56
P(ACD) = AC + CD + DA = 60
=> P (ABC) + P(ACD) = (AB + BC + CD + DA) + 2.AC = 66 + 2.AC = 56 + 60 = 116
=> 2.AC = 116 - 66 = 50 => AC = 50 : 2 = 25

AB+BC+CD+AD=70
AB+AD+BD=50
CD+BD+BC=60
=>AB+BC+CD+AD+2BD=50+60=110
=>70+2BD=110
=>2BD=40=>BD=20(cm)

∆ABC ∽ ∆A'B'C' => ABA′B′ABA′B′ = BCB′C′BCB′C′= CAC′A′CAC′A′ = CABCCA′B′C′CABCCA′B′C′
hay 3A′B′3A′B′ = 7B′C′7B′C′ = 5A′C′5A′C′ = CABC55CABC55 = 311311
=> A'B' = 11cm;
B'C' = 7.1137.113 ≈ 25.67 cm
A'C' = 5.1135.113 ≈ 18,33 cm

Vì tam giác \(ABC\) đồng dạng với tam giác \(A'B'C'\) nên tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\). Do đó, \(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{{A'B'}}{4} = \frac{{B'C'}}{9} = \frac{{A'C'}}{6}\). Áp dụng tính chất dãy tỉ số bằng nhau ta được:
\(\frac{{A'B'}}{4} = \frac{{B'C'}}{9} = \frac{{A'C'}}{6} = \frac{{A'B' + B'C' + A'C'}}{{4 + 6 + 9}} = \frac{{66,5}}{{19}} = 3,5\)
Ta có:
\(\left\{ \begin{array}{l}\frac{{A'B'}}{4} = 3,5 \Rightarrow A'B' = 3,5.4 = 14\\\frac{{A'C'}}{6} = 3,5 \Rightarrow A'C' = 3,5.6 = 21\\\frac{{B'C'}}{9} = 3,5 \Rightarrow B'C' = 3,5.9 = 31,5\end{array} \right.\)
Vậy \(A'B' = 14cm,A'C' = 21cm,B'C' = 31,5cm\).

Bài giải :
_ Gọi chu vi là P .
Ta có : \(P\)Tứ giác \(ABCD=\)\(AB+BC+CD+DA=66.\)
\(P\)Tam giác \(ABC\)\(=AB+BC+CA=56.\)
\(P\)Tam giác \(ACD=\)\(AC+CD+CA=60.\)
\(\Rightarrow P\)Tam giác \(ABC+ADC\)
\(\rightarrow\left(AB+BC+CD+DA\right)\)\(+2\times AC\)
\(=66+2\times AC\)
\(=56+60\)
\(=116.\)
\(\Rightarrow2\times AC\)
\(=116-66\)
\(=50.\)
\(\Rightarrow AC=50\div2\)
\(=25.\)