Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔABC có
BM,CN lần lượt là các đường trung tuyến
BM cắt CN tại I
=>I là trọng tâm
=>AI là đường trung tuyến của ΔACB
ΔABC cân tại A
mà AI là đường trung tuyến
nên AI vuông góc CB
=>AI là trung trực của BC

Xét tam giác ABD và ACD có
AB=AC (tam giác ABC cân tại A)
Góc B = góc C ( 2 góc ở đáy của tam giác cân)
Canh AD chung
Suy ra tam giác ABD= tam giác ACD
Nen goc BAD=CAD(2 goc tuong ung)
Nên AD là tia phân giác của góc A
Suy ra AD là đường phân giác ,đường cao,đường trung trực,đường trung tuyến(tính chất tam giác cân)

a: Xet ΔABI và ΔACI có
AB=AC
BI=CI
AI chung
=>ΔABI=ΔACI
b: ΔABC cân tại A
mà AI là trung tuyến
nên AI vuông góc BC
c: GI=1/3*AI=4cm

AB:=a
AC:=b
ta có
BD^2=a^2+(1/2b)^2
CE^2=(1/2a)^2+b^2
BD^2+CE^2=(a^2+b^2)5/4=5/4BC^2(dpcm)

`a,`
Vì `\Delta ABC` cân tại A
`-> \text {AB = AC, }` $\widehat {B} = \widehat {C}$
Xét `\Delta ABH` và `\Delta ACH`:
`\text {AB = AC}`
$\widehat {B} = \widehat {C}$
$\widehat {AHB} = \widehat {AHC} (=90^0) (\text {AH là đường cao của} \Delta ABC)$
`=> \Delta ABH = \Delta ACH (ch-gn)`
`b,`
Vì `\Delta ABH = \Delta ACH (a)`
`->` $\widehat {BAH} = \widehat {CAH} (\text {2 cạnh tương ứng})$
`-> \text {AH là đường phân giác của}` `\Delta ABC`
`c,`
Vì `\Delta ABH = \Delta ACH (a)`
`-> \text {HB = HC}`
Ta có:
`\text {AH} \bot \text {BC}`
`\text {HB = HC}`
`-> \text {AH là đường trung trực của}` `\Delta ABC`.
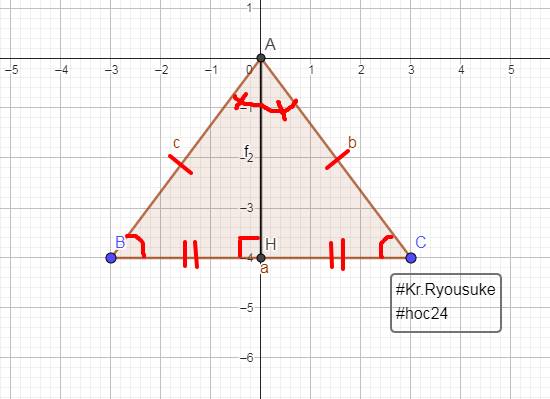

Xét ΔAIB và ΔAIC có
AI chung
IB=IC
AB=AC
Do đó: ΔAIB=ΔAIC
=>\(\widehat{AIB}=\widehat{AIC}\)
mà \(\widehat{AIB}+\widehat{AIC}=180^0\)(hai góc kề bù)
nên \(\widehat{AIB}=\widehat{AIC}=\dfrac{180^0}{2}=90^0\)
=>AI\(\perp\)BC