Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔABD và ΔACD có
AB=AC(ΔABC cân tại A)
\(\widehat{BAD}=\widehat{CAD}\)(AD là tia phân giác của \(\widehat{BAC}\))
AD chung
Do đó: ΔABD=ΔACD(c-g-c)
Suy ra: \(\widehat{ADB}=\widehat{ADC}\)(hai góc tương ứng)
mà \(\widehat{ADB}+\widehat{ADC}=180^0\)(hai góc kề bù)
nên \(\widehat{ADB}=\widehat{ADC}=\dfrac{180^0}{2}=90^0\)
hay \(\widehat{ADM}=90^0\)
Xét ΔADM có DA=DM(gt)
nên ΔADM cân tại D(Định nghĩa tam giác cân)
Xét ΔADM cân tại D có \(\widehat{ADM}=90^0\)(cmt)
nên ΔADM vuông cân tại D(Định nghĩa tam giác vuông cân)

Trả lời:
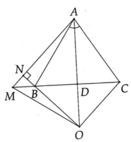
A B C D M N O
a, Tam giác ABC cân tại A có: AD là đường phân giác của ^BAC
=> AD đồng thời là đường trung trực của của tam giác ABC
=> AD \(\perp\)BC
=> tam giác DAM vuông tại D (đpcm)
b, Xét tam giác AMO có:
ON là đường cao thứ nhất ( ON \(\perp\)AM )
MD là đường cao thứ hai ( MD \(\perp\)AO )
Mà ON và BN cắt nhau tại B
=> B là trực tâm của tam giác AMO
=> AB là đường cao thứ ba
=> AB \(\perp\)OM (đpcm)
c, Tam giác BCO có:
AD là đường trung trực hay OD là đường trung trực ứng với canh BC
=> O cách đều 2 đầu mút B và C
=> OB = OC (đpcm)

a: Xét ΔBDA vuông tại D và ΔBEC vuông tại E có
BA=BC
góc B chung
=>ΔBDA=ΔBEC
b: ΔBDA=ΔBEC
=>BE=BD
=>ΔBED cân tại B
c: Xét ΔCAM có
CD vừa là đường cao, vừa là trung tuyến
=>ΔCAM cân tại C
=>góc CMD=góc CAM=góc ECA

a: Xét ΔAMD vuông tại M và ΔAND vuông tại N có
AD chung
góc MAD=góc NAD
=>ΔMAD=ΔNAD
=>AM=AN
b: Xét ΔACB có AM/AB=AN/AC
nên MN//BC
c: Xét ΔADE có
AM vừa là đường cao, vừa là trung tuýen
=>ΔADE cân tại A
=>AD=AE
Xét ΔADF có
AN vừa là đường cao, vừa là trung tuyến
=>ΔADF cân tại A
=>AD=AF
=>AE=AF
=>ΔAEFcân tạiA

Bạn tự vẽ hình nha
AED + DEC = 180
mà DEC = AEF (tam giác AFE = tam giác DCE)
=> AED + AEF = 180
=> EF và ED là 2 tia đối
=> D , E , F thẳng hàng