Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

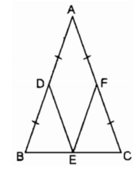
Ta có: E là trung điểm của BC (gt)
D là trung điểm của AB (gt) nên ED là đường trung bình của ∆ ABC
DE = AF = 1/2 AC (1)
F là trung điểm của AC (gt) nên EF là đường trung bình ∆ ABC ⇒ EF = AD = 1/2 AB (2)
AB = AC (gt)
Từ (1), (2) và (gt) suy ra: AD = DE = EF = AF
Vậy tứ giác ADEF là hình thoi.

a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC

Bài 2:
a: Xet ΔABC có AD/AB=AF/AC
nen DF//BC và DF=1/2BC
=>BDFC là hình thang
mà góc B=góc C
nên BDFC là hình thang cân
b Xet ΔABC có
CE/CB=CF/CA
nên EF//AB và EF=AB/2
=>EF//AD và EF=AD
=>ADEF là hình bình hành
mà AD=AF
nen ADEF là hình thoi
c: Để ADEF là hình vuông thì góc BAC=90 độ

Hình bạn tự vẽ nhé!
Có: `M,N` là trung điểm của `AB,AC`
`=>MN` là đường trung bình của `\DeltaABC`
`=> MN //// BC`
Tương tự: `MD,ND` là đường trung bình của `\DeltaABC`.
`=> MD //// AC ; ND ////AB`
`=> MD //// AN ; ND //// AM`
`=>` Tứ giác `AMDN` là hình bình hành. (1)
Xét `\DeltaABC` cân tại `A` có: `D` là trung điểm của `BC`
`=> AD` vừa là trung tuyến, vừa là đường cao.
`=> AD \bot BC`
Mà `BC////MN`
`=> AD \bot MN`. (2)
Từ (1) và (2) `=> AMDN` là hình thoi.
theo bài ra AB,AC,BC là có các trung điểm thứ tự M,N,D
=>AM=MB,AN=NC,BD=DC
=>MN là đường trung bình tam giác ABC=>MN//BC
=>MD là...................................................=>MD//AC
=>ND là....................................................=>ND//AB
=>AMDN là hình bình hành,
gọi giao điểm MN và AD là K
mà AMDN là hình bình hành nên MN và AD cắt nhau tại trung điểm K mỗi đường (1)
Do tam giác ABC cân có AD là trung tuyến nên đồng thời là đường cao
\(=>AD\perp BC\) mà MN//BC=>\(AD\perp MN\)(2)
từ (1)(2)=>AMDN là hình thoi