Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

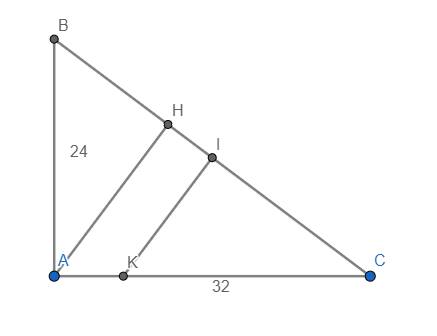
Ta có \(\widehat{HAC}=\widehat{B}\) (cùng phụ với \(\widehat{C}\))
Mà \(\widehat{B}=\tan^{-1}\left(\dfrac{AC}{AB}\right)=\tan^{-1}\left(\dfrac{32}{24}\right)=\tan^{-1}\left(\dfrac{4}{3}\right)\approx53,13^o\)
Nên \(\widehat{HAC}\approx53,13^o\)
Ta có \(BC=\sqrt{AB^2+AC^2}=\sqrt{24^2+32^2}=40\) cm
\(\Rightarrow IB=IC=20cm\)
Ta có \(CH=\dfrac{AC^2}{BC}=\dfrac{32^2}{40}=25,6cm\)
\(AH=\dfrac{AB.AC}{BC}=\dfrac{24.32}{40}=19,2cm\)
Do vậy \(\dfrac{CI}{CH}=\dfrac{IK}{AH}\Rightarrow IK=\dfrac{CI.AH}{CH}=\dfrac{20.19,2}{25,6}=15cm\)
Mặt khác \(\dfrac{CI}{CH}=\dfrac{CK}{CA}\Rightarrow CK=\dfrac{CI.CA}{CH}=\dfrac{20.32}{25,6}=25cm\)
\(\Rightarrow C_{CIK}=CI+CK+IK\) \(=20+15+25=60cm\)
Mặt khác, \(S_{ABC}=\dfrac{1}{2}AB.AC=\dfrac{1}{2}.24.32=384cm^2\)
Lại có \(\Delta CIK~\Delta CAB\left(g.g\right)\) \(\Rightarrow\dfrac{S_{CIK}}{S_{CAB}}=\left(\dfrac{IK}{AB}\right)^2=\left(\dfrac{15}{24}\right)^2=\dfrac{25}{64}\)
\(\Rightarrow S_{CIK}=\dfrac{25}{64}S_{CAB}=\dfrac{25}{64}.384=150cm^2\)

Cậu tự vẽ hình nhé
a, kẻ MK vuông BC, NG vuông BC
Tam g ABC cân => g ABC= g ACB
Lại có g ACB = g GCN (dd)
=> g GCN = g ABC=g MBK
Xét tg MBK và tg NCG
g MKB= g NGC =90°
g MBK = g NCG (cmt)
MB= CN(gt)
=> tg MBK= tg NCG ( ch-gn)
=> MK=NG (2 cạnh tương ứng)
Vì MK vuông BC, NG vuông BC => NG// MK
=> g GNM = g KMN ( so le trong )
Xét tg MKD VÀ TG NGD
g MKD = g DGN = 90°
g KMD = gDNG ( cmt)
Mk= GN (cmt)
=> tg MKD = tg NGD (_cgv-gn)
=> MD= ND (2 ctu)
=> D là td MN ( dpcm)
Xét tam giác cân ABC , AH là đường cao => AH là trung trực
Lại có E thuộc AH => EC= EB
Xét tg ABE và tg ACE
AB=AC (tg ABC cân)
BE= EC (cmt)
AE cạnh chung
=> tg ABE = tg ACE (ccc)
=> g ABE = g ACE ( 2 góc tương ứng)(1)
Lại có DE là trung trực MN => ME = NE
Xét tg MBE và tg NCE
MB = NC ( gt)
ME = NE (cmt)
BE = CE (cmt)
=> tg MBE = tg NCE (ccc)
=> g ECN = g EBM (2 góc t u ) (2)
Từ 1), 2) => g ECA = g ECN
Lại có 2 góc này bù nhau
=>g ACE= 90°= g ABE
Xét tg ABE vuông
+ theo đl pytago:
=> AE = √( ab2+bE2)= √( 62+4,52)= 7,5 (cmcm)
+ BH là đcao, theo hệ thức lượng trong tg vuông
=>+ AB2= AH.AE => AH= 62:7,5=4,8 (cmcm)
+ 1/(BH2)= 1/(AB2)+1/(BE2) => BH = √(1:( (1/62)+(1/4,52))= 3,6(ccmcm)
=> BC= 3,6.2= 7,2 (cm)
=> dt tg ABC có đcao AH là 7,2.4,8.1/2= 28,08(cm2)
Vậy S tg ABC = 28,08 cm2

Xét \(\Delta\)ABC cân tại A có :
AH là đường cao
\(\Rightarrow\)AH là đường trung tuyến
\(\Rightarrow\)H là trung điểm của BC
\(\Rightarrow\)BH = HC =\(\dfrac{BC}{2}\)\(\dfrac{16}{2}=8\)
Xét \(\Delta\)AHB vuông tại H có:
\(\cos\)B=\(\dfrac{BH}{AB}=\dfrac{8}{10}\)=0.8
\(\Rightarrow\Lambda B\approx37\)độ
Ta có : góc B = góc C (Tam giác ABC cân tại A)
Mà góc B\(\approx37\)độ
\(\Rightarrow\)góc C\(\approx\)37 độ
b, Xét \(\Delta\)ABC có :
góc BAC+gócACB+góc ABC=180
\(\Rightarrow\)góc BAC=106 độ
Xét \(\Delta\)AHB vuông tại H có :
\(AB^2=AH^2+HB^2\Rightarrow AH=6\)
Ta có \(AI=\dfrac{1}{3}AH\Rightarrow HI=\dfrac{2}{3}AH\)
\(\Rightarrow\)HI=4cm
Xét tam giác BDC có
\(HI\) song song CD
\(\Rightarrow\dfrac{HI}{CD}=\dfrac{BH}{CH}=\dfrac{8}{16}=\dfrac{1}{2}\)
\(CD=8cm\)
Xét tứ giác AHCD có :
AH song somg CD
\(\Rightarrow\)AHCD là hình thang
Diện tích hình thang AHCD là :
\(\dfrac{1}{2}\left(6+8\right)\times8=56cm^2\)
Diện tích AHB là :
\(\dfrac{1}{2}\times6\times8=24cm^2\)
Diện tích tứ giác ABCD là
\(56+24=80cm^2\)