Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 7:
Giải:
Giá tiền của mỗi chiếc máy tính bán trong đợt đầu là:
8 x (100% + 30%) = 10,4(triệu đồng)
Tổng số tiền thu được khi bán 70 chiếc máy tính trong đợt đầu là:
10,4 x 70 = 728 (triệu đồng)
Giá của mỗi chiếc máy tính bán được trong đợt sau là:
10,4 x 65% = 6,76(triệu đồng)
Số tiền thu được khi bán hết số máy tính còn lại là:
6,76 x (100 - 70) = 202,8 (triệu đồng)
Tổng số tiền mà cửa hàng thu được khi bán hết 100 cái máy tính là:
728 + 202,8 = 930,8 (triệu đồng)
Tiền vốn của 100 cái máy tính là:
8 x 100 = 800 (triệu đồng)
Sau khi bán hết 100 máy tính thì người đó lãi và lãi số tiền là:
930,8 - 800 = 130,8 (triệu đồng)
Kết luận: Sau khi bán hết 100 máy tính người đó lãi và lãi số tiền là 130,8 triệu đồng
Bài 8:
a; Doanh thu năm 2019 là: 5,6 x \(\frac34\) = 4,2 (triệu usd)
b; Sau năm năm để lời 7,8 triệu usd thì năm 2020 phải thu được:
7,8 - (-1,8 + 5,6 - 3,6 + 4,2) = 3,4(triệu usd)
Kết luận: năm 2019 thu 4,2 triệu usd
năm 2020 thu 3,4 triệu usd

a: Ta có: \(\hat{AOD}+\hat{BOD}=180^0\) (hai góc kề bù)
=>\(\hat{BOD}=180^0-97^0=83^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia OA, ta có: \(\hat{AOE}<\hat{AOD}\left(56^0<97^0\right)\)
nên tia OE nằm giữa hai tia OA và OD
=>\(\hat{AOE}+\hat{EOD}=\hat{AOD}\)
=>\(\hat{EOD}=97^0-56^0=41^0\)
Ta có: \(\hat{AOE}+\hat{EOC}+\hat{COB}=180^0\)
=>\(\hat{EOC}=180^0-56^0-42^0=82^0\)
b: Trên cùng một nửa mặt phẳng bờ chứa tia OE, ta có; \(\hat{EOD}<\hat{EOC}\left(41^0<82^0\right)\)
nên tia OD nằm giữa hai tia OE và OC
=>\(\hat{EOD}+\hat{DOC}=\hat{EOC}\)
=>\(\hat{DOC}=82^0-41^0=41^0\)
Ta có: tia OD nằm giữa hai tia OE và OC
\(\hat{DOE}=\hat{DOC}\left(=41^0\right)\)
Do đó: OD là phân giác của góc EOC

a: Ta có: \(3x+\left(x-\frac{9}{20}\right)=-\frac{13}{40}\)
=>\(3x+x-\frac{9}{20}=-\frac{13}{40}\)
=>\(4x=-\frac{13}{40}+\frac{9}{20}=-\frac{13}{40}+\frac{18}{40}=\frac{5}{40}=\frac18\)
=>\(x=\frac18:4=\frac{1}{32}\)
b: \(x+\left(\frac14x-2,5\right)=-\frac{11}{20}\)
=>\(x+\frac14x-2,5=-\frac{11}{20}\)
=>\(1,25x=-0,55+2,5=1,95\)
=>\(x=\frac{1.95}{1.25}=\frac{195}{125}=\frac{39}{25}\)
c: \(\frac35x+\left(x+0,5\right)=-\frac{13}{15}\)
=>\(\frac35x+x+0,5=-\frac{13}{15}\)
=>\(\frac85x=-\frac{13}{15}-0,5=-\frac{26}{30}-\frac{15}{30}=-\frac{41}{30}\)
=>\(x=-\frac{41}{30}:\frac85=-\frac{41}{30}\cdot\frac58=\frac{-41}{6\cdot8}=-\frac{41}{48}\)
d: \(-\frac23x+\left(4x-\frac67\right)=\frac{9}{21}\)
=>\(-\frac23x+4x-\frac67=\frac37\)
=>\(\frac{10}{3}x=\frac37+\frac67=\frac97\)
=>\(x=\frac97:\frac{10}{3}=\frac97\cdot\frac{3}{10}=\frac{27}{70}\)
bài 11: câu a:
\(3x+\left(x-\frac{9}{20}\right)=-\frac{13}{40}\)
\(3x+x-\frac{9}{20}=-\frac{13}{40}\)
\(4x=-\frac{13}{40}+\frac{9}{20}\)
\(4x=-\frac{13}{40}+\frac{18}{40}\)
\(4x=\frac{5}{40}\)
\(4x=\frac18\)
\(x=\frac18:4=\frac18\cdot\frac14=\frac{1}{32}\)
b. \(x+\left(\frac14x-2,5\right)=-\frac{11}{20}\)
\(x+\frac14x-2,5=-\frac{11}{20}\)
\(\frac54x-2,5=-\frac{11}{20}\)
\(\frac54x=-\frac{11}{20}+2,5\)
\(\frac54x=\frac{39}{20}\)
\(x=\frac{39}{20}:\frac54=\frac{39}{20}\cdot\frac45=\frac{39}{25}\)
c. \(\frac35x+\left(x+0,5\right)=-\frac{13}{15}\)
\(\frac35x+x+0,5=-\frac{13}{15}\)
\(\frac85x+\frac12=-\frac{13}{15}\)
\(\frac85x=-\frac{13}{15}-\frac12\)
\(\frac85x=-\frac{41}{30}\)
\(x=-\frac{41}{30}:\frac85=-\frac{41}{30}\cdot\frac58=-\frac{41}{48}\)
\(d.-\frac23x+\left(4x-\frac67\right)=\frac{9}{21}\)
\(-\frac23x+4x-\frac67=\frac{9}{21}\)
\(\frac{10}{3}x=\frac97\)
\(x=\frac97:\frac{10}{3}=\frac97\cdot\frac{3}{10}=\frac{27}{70}\)

d: \(\left(-\frac34+\frac25\right):\frac37+\left(\frac35-\frac14\right):\frac37\)
\(=\left(-\frac34+\frac25+\frac35-\frac14\right):\frac37\)
\(=\left(1-1\right):\frac37=0\)
e: \(\frac59:\left(\frac{1}{11}-\frac{5}{22}\right)+\frac59:\left(\frac{1}{15}-\frac23\right)\)
\(=\frac59:\left(\frac{2}{22}-\frac{5}{22}\right)+\frac59:\left(\frac{1}{15}-\frac{10}{15}\right)\)
\(=\frac59:\frac{-3}{22}+\frac59:\frac{-9}{15}\)
\(=\frac59\cdot\frac{-22}{3}+\frac59\cdot\frac{-5}{3}=\frac59\left(-\frac{22}{3}-\frac53\right)=\frac59\cdot\frac{-27}{3}=-5\)

a: \(\left(-\frac54x+3,25\right)\left\lbrack\frac35-\left(-\frac52x\right)\right\rbrack=0\)
=>\(\left(\frac54x-\frac{13}{4}\right)\left(\frac52x+\frac35\right)=0\)
=>\(\left[\begin{array}{l}\frac54x-\frac{13}{4}=0\\ \frac52x+\frac35=0\end{array}\right.\Rightarrow\left[\begin{array}{l}\frac54x=\frac{13}{4}\\ \frac52x=-\frac35\end{array}\right.\Rightarrow\left[\begin{array}{l}x=\frac{13}{4}:\frac54=\frac{13}{5}\\ x=-\frac35:\frac52=-\frac{6}{25}\end{array}\right.\)
b: \(\left(-\frac72x+1,75\right)\left\lbrack\frac45-\left(-\frac53x\right)\right\rbrack=0\)
=>\(\left[\begin{array}{l}-\frac72x+1,75=0\\ \frac45-\left(-\frac53x\right)=0\end{array}\right.\Longrightarrow\left[\begin{array}{l}-\frac72x=-1,75=-\frac74\\ \frac53x=-\frac45\end{array}\right.\)
=>\(\left[\begin{array}{l}x=\frac{-7}{4}:\frac{-7}{2}=\frac24=\frac12\\ x=-\frac45:\frac53=-\frac45\cdot\frac35=-\frac{12}{25}\end{array}\right.\)
c: \(\left(x^2-4\right)\left(x+\frac27\right)=0\)
=>\(\left[\begin{array}{l}x^2-4=0\\ x+\frac27=0\end{array}\right.\Rightarrow\left[\begin{array}{l}x^2=4\\ x=-\frac27\end{array}\right.\Rightarrow\left[\begin{array}{l}x=2\\ x=-2\\ x=-\frac27\end{array}\right.\)
d: \(\left(25-x^2\right)\left(5x-\frac59\right)=0\)
=>\(\left[\begin{array}{l}25-x^2=0\\ 5x-\frac59=0\end{array}\right.\Rightarrow\left[\begin{array}{l}x^2=25\\ 5x=\frac59\end{array}\right.\Rightarrow\left[\begin{array}{l}x=5\\ x=-5\\ x=\frac19\end{array}\right.\)

Bài 2:
Qua B, kẻ tia BD nằm giữa hai tia BA và BC sao cho BD//Ax//Cz
ta có: BD//Ax
=>\(\hat{xAB}+\hat{ABD}=180^0\) (hai góc trong cùng phía)
=>\(\hat{ABD}=180^0-125^0=55^0\)
Ta có: BD//Cz
=>\(\hat{DBC}+\hat{BCz}=180^0\) (hai góc trong cùng phía)
=>\(\hat{DBC}=180^0-130^0=50^0\)
Ta có: tia BD nằm giữa hai tia BA và BC
=>\(\hat{ABC}=\hat{DBA}+\hat{DBC}\)
=>\(\hat{ABC}=55^0+50^0=105^0\)
Bài 3:
Ax//yy'
=>\(\hat{xAB}=\hat{yBA}\) (hai góc so le trong)
=>\(\hat{yBA}=50^0\)
Cz//yy'
=>\(\hat{yBC}=\hat{zCB}\) (hai góc so le trong)
=>\(\hat{yBC}=40^0\)
Ta có: tia By nằm giữa hai tia BA và BC
=>\(\hat{ABC}=\hat{yBA}+\hat{yBC}=40^0+50^0=90^0\)
Bài 4:
Qua B, kẻ tia BD nằm giữa hai tia BA và BC sao cho BD//Ax//Cz
BD//Ax
=>\(\hat{xAB}+\hat{ABD}=180^0\) (hai góc trong cùng phía)
=>\(\hat{ABD}=180^0-110^0=70^0\)
ta có; tia BD nằm giữa hai tia BA và BC
=>\(\hat{DBA}+\hat{DBC}=\hat{ABC}\)
=>\(\hat{DBC}=100^0-70^0=30^0\)
Ta có: \(\hat{DBC}=\hat{zCB}\left(=30^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên BD//Cz
Ta có: BD//Ax
BD//Cz
Do đó: Ax//Cz

a: a//b
=>\(\hat{A_1}=\hat{B_3}\) (hai góc so le trong)
mà \(\hat{A_1}=65^0\)
nên \(\hat{B_3}=65^0\)
b: Ta có: \(\hat{B}_3+\hat{B_2}=180^0\) (hai góc kề bù)
=>\(\hat{B_2}=180^0-65^0=115^0\)
Giải:
a; \(\hat{A_1}\) = \(65^0\) (gt)
\(\hat{A_1}\) = \(\hat{A_3}\) = 65\(^0\)(đối đỉnh)
\(\hat{A_3}\) = \(\hat{B_3}\) = \(65^0\) (slt)
b; \(\hat{B_2}\) + \(\hat{B_3}\) = 180\(^0\) (hai góc kề bù)
\(\hat{B_2}\) = 180\(^0\) - \(\hat{B_3}\)
\(\hat{B_2}\) = 180\(^0\) - 65\(^0\) = 115\(^0\)
Vậy a; \(\hat{B}_3\) = 65\(^0\)
b; \(\hat{B_2}\) = 115\(^0\)


\(a.\frac12+\frac32x=\frac34\)
\(\frac32x=\frac34-\frac12=\frac14\)
\(x=\frac14:\frac32=\frac14\cdot\frac23=\frac16\)
\(b.2,5-2\cdot\left(x-0,5\right)=2\)
\(2\cdot\left(x-0,5\right)=2,5-2=0,5\)
\(x-0,5=0,5:2=0,25\)
\(x=0,25+0,5=0,75\)
\(c.\left(x+\frac32\right)^3=\frac{125}{8}=\left(\frac52\right)^3\)
\(x+\frac32=\frac52\)
\(x=\frac52-\frac32=\frac22=1\)
\(d.\left(x-\frac13\right)^2=\frac{25}{4}=\left(\pm\frac52\right)^2\)
\(\left[\begin{array}{l}x-\frac13=\frac52\Rightarrow x=\frac{17}{6}\\ x-\frac13=-\frac52\Rightarrow x=-\frac{13}{6}\end{array}\right.\)
vậy \(x\in\left\lbrace\frac{17}{6};-\frac{13}{6}\right\rbrace\)
\(e.7\cdot3^{x-1}-3^{x+2}=-540\)
\(3^{x-1}\cdot\left(7-3^3\right)=-540\)
\(3^{x-1}\cdot\left(7-27\right)=-540\)
\(3^{x-1}\cdot\left(-20\right)=-540\)
\(3^{x-1}=\left(-540\right):\left(-20\right)\)
\(3^{x-1}=27=3^3\)
⇒ x - 1 = 3
⇒ x = 4
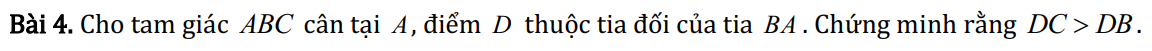












Bài 4:
Xét ΔABC có \(\widehat{CBD}\) là góc ngoài tại đỉnh B
nên \(\widehat{CBD}=\widehat{BCA}+\widehat{BAC}\)
=>\(\widehat{CBD}>\widehat{ACB}\)
mà \(\widehat{ACB}=\widehat{ABC}\)(ΔABC cân tại A)
nên \(\widehat{CBD}>\widehat{CBA}\)
mà \(\widehat{CBD}+\widehat{CBA}=180^0\)
nên \(\widehat{CBD}>\dfrac{180^0}{2}=90^0\)
Xét ΔCBD có \(\widehat{CBD}>90^0\)
nên CD là cạnh lớn nhất trong ΔCBD
=>CD>CB