Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
đừng tích ai nhá, tôi về mình giải cho, giờ mik phải đi học thêm
ΔABD cân tại B có 
ΔACE cân tại C có 
Answer:
Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow100^o+\widehat{C}+\widehat{B}=180^o\)
\(\Rightarrow2\widehat{B}=80^o\)
\(\Rightarrow\widehat{B}=\widehat{C}=40^o\)
Ta có: Tam giác ACE cân tại C
Mà: \(\widehat{A}+\widehat{C}+\widehat{E}=180^o\)
\(\Rightarrow2\widehat{E}+40^o=180^o\)
\(\Rightarrow2\widehat{E}=140^o\)
\(\Rightarrow\widehat{E}=70^o\) (1)
Ta có: Tam giác ABD cân tại B
Mà: \(\widehat{A}+\widehat{B}+\widehat{D}=180^o\)
\(\Rightarrow2\widehat{D}+40^o=180^o\)
\(\Rightarrow2\widehat{D}=140^o\)
\(\Rightarrow\widehat{D}=70^o\) (2)
Từ (1) và (2) \(\Rightarrow\widehat{A}+\widehat{E}+\widehat{D}=180^o\)
\(\Rightarrow\widehat{A}+2.70^o=180^o\)
\(\Rightarrow\widehat{A}+140^o=180^o\)
\(\Rightarrow\widehat{A}=40^o\)
Vậy \(\widehat{DAE}=40^o\)
ΔABD cân tại B có
ΔACE cân tại C có
+) Ta có:
(tổng ba góc trong 1 tam giác)
Lại có: tam giác ABC là tam giác cân tại A nên:
+)Xét tam giác ABD có BA= BD (giả thiết) nên tam giác ABD cân tại B.
Lại có; 
( tổng ba góc trong 1 tam giác)
+) Tương tự, ta có tam giác AEC cân tại C ( vì CA =CE)
+) Xét tam giác ADE có:
( tổng ba góc trong tam giác)
Suy ra:
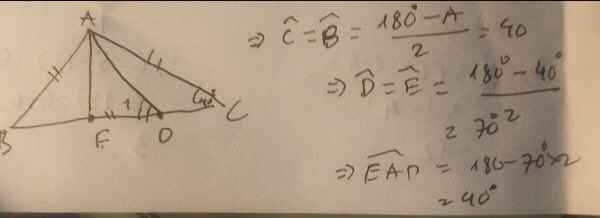
Vì \(\Delta ABC\)cân tại \(A\left(gt\right)\)
\(\Rightarrow\widehat{B}=\widehat{C}\)( tính chất tam giác cân )
\(\Rightarrow\widehat{B}=\widehat{C}=\frac{180^0-\widehat{A}}{2}\)
\(\Rightarrow\widehat{B}=\widehat{C}=\frac{180^0-100^0}{2}=\frac{80^0}{2}=40^0\)
Xét \(\Delta ABD\)có:
\(BD=BA\left(gt\right)\)
\(\Rightarrow\Delta ABD\)cân tại B
\(\Rightarrow\widehat{BAD}=\widehat{ADB}\)( tính chất tam giác cân )
\(\Rightarrow\widehat{BAD}=\widehat{ADB}=\frac{180^0-\widehat{B}}{2}\)
\(\Rightarrow\widehat{BAD}=\widehat{ADB}=\frac{180^0-40^0}{2}=\frac{140^0}{2}=70^0\)
\(\Rightarrow\widehat{ADB}=70^0\)
Hay \(\widehat{ADE}=70^0\)
Xét \(\Delta ADE\)có:
\(\widehat{DAE}+\widehat{ADE}+\widehat{AED}=180^0\)( định lý tổng 3 góc trong 1 tam giác )
\(\Rightarrow\widehat{DAE}+70^0+70^0=180^0\)
\(\Rightarrow\widehat{DAE}+140^0=180^0\)
\(\Rightarrow\widehat{DAE}=180^0-140^0\)
\(\Rightarrow\widehat{DAE}=40^0\)
Vậy \(\widehat{DAE}=40^0\)
Hình vẽ: