Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C M
a) Xét t/giác ABM và t.giác ACM
có: AB = AC (gt)
AM : chung
BM = MC (gt)
=> t/giác ABM = t/giác ACM (c.c.c)
=> \(\widehat{AMB}=\widehat{AMC}\) (2 góc t/ứng)
Mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(kề bù)
=> \(\widehat{AMB}=\widehat{AMC}=90^0\)
=> AM vuông góc với BC
b) Ta có: BM = MC = 1/2BC = 1/2.32 = 16 (cm)
Áp dụng định lí Pi - ta - go vào t/giác ABM vuông tại M, ta có:
\(AB^2=AM^2+BM^2\)
=> AM2 = AB2 - BM2 = 342 - 162 = 900
=> AM = 30 (cm)
c) Chu vi t/giác AMB = 34 + 16 + 30 = 80 (cm)
Diện tích t/giác ABM là: 30 x 16 : 2 = 240 (cm2)

Cho tam giác ABC cân ở A, đường trung tuyến AM.
a) Chứng minh AM BC
b) Tính AM biết rằng AB cm BC cm 10 , 12

Trả lời:
P/s: Học kém Hình nên chỉ đucợ mỗi câu a
a, +Xét tam giác ABM và ACM có:
AB=AC(Giả thiết) --
AM là cạnh chung) I =>tam giác ABM=ACM (C-C-C)
~Học tốt!~

Xét \(\Delta MBE\)và \(\Delta MAE\)ta có :
\(ME\): cạnh chung (1)
Góc \(MEB=MEA=90\)độ (2)
\(MB=MA\left(GT\right)\) (3)
Từ (1) ; (2) và (3) => \(\Delta MBE=\Delta MAE\)(cạnh-góc-cạnh)
\(\Rightarrow MB=MA\)( cặp cạnh tương ứng)
b) Áp dụng định lí Py-ta-go cho tam giác vuông BAC có:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow8^2+6^2=BC^2\)
\(\Rightarrow64+36=BC^2\)
\(\Rightarrow100=BC^2\)
\(\Rightarrow\)BC= Căn 100
\(\Rightarrow BC=10\)
Vậy BC = 10 cm .

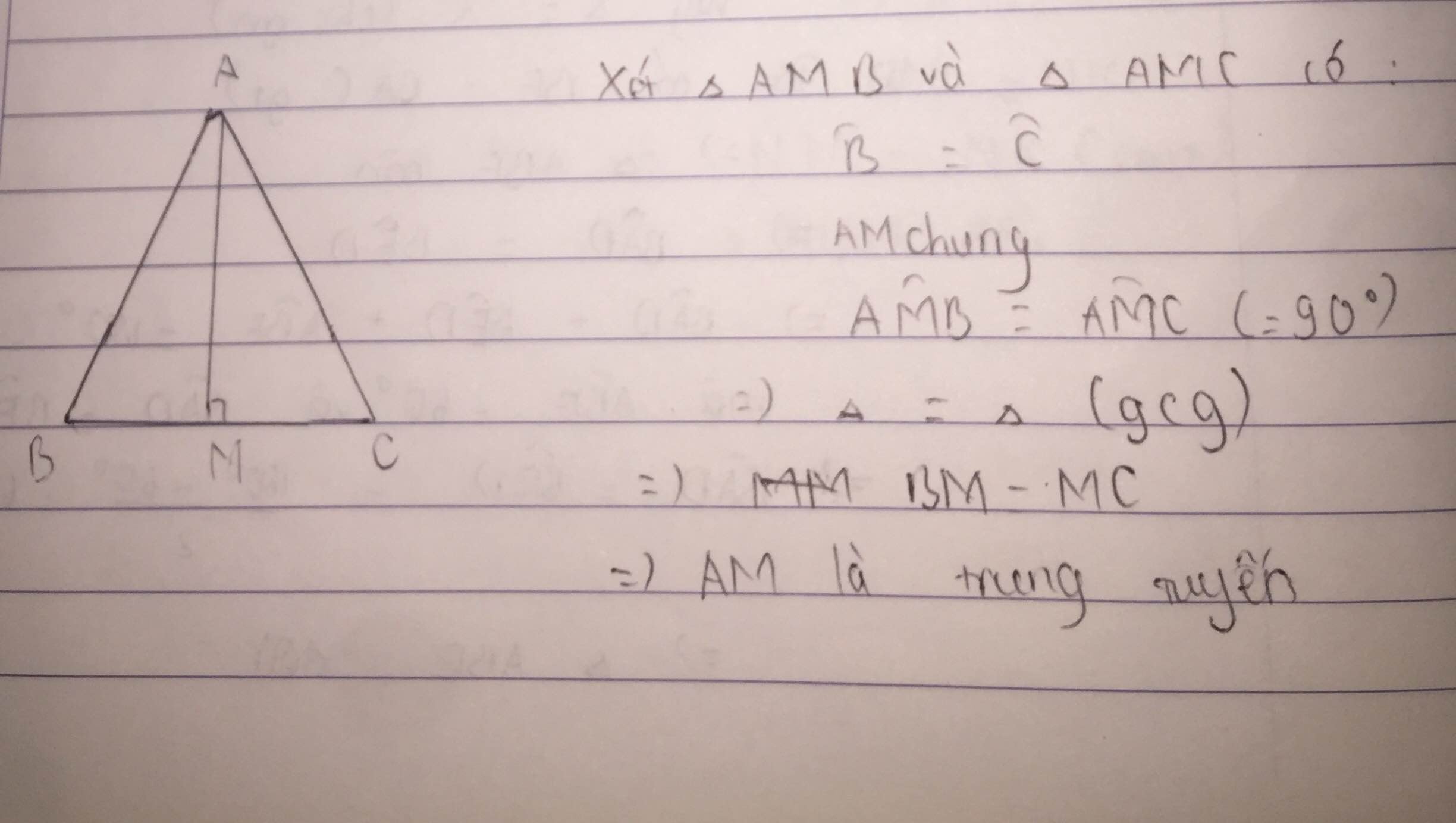
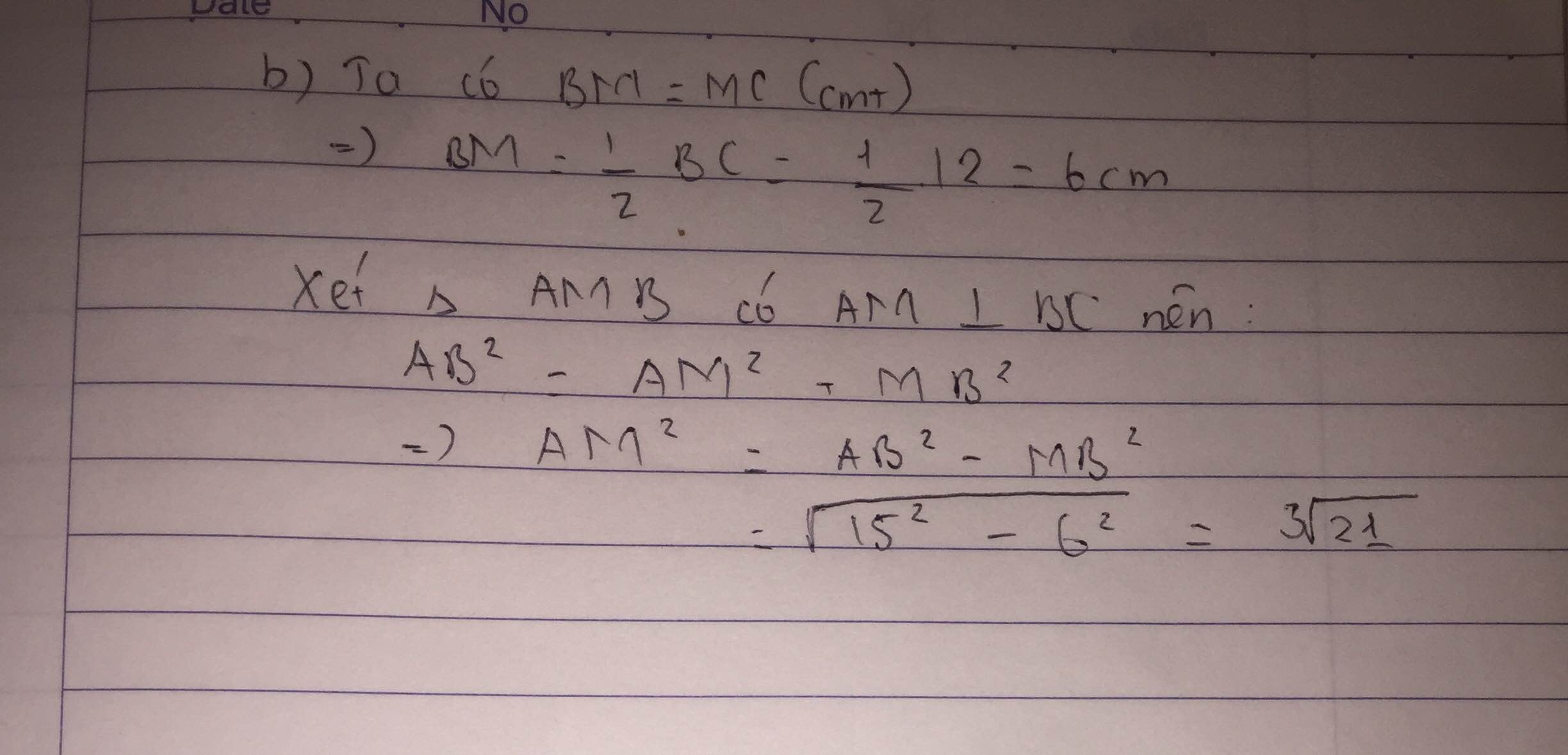
a/Ta có: ΔABC cân ở A(gt)
mà AM là đường trung tuyến, nên AM cũng là đường cao
Vậy AM ⊥ BC
b/ Vì M là trung điểm của BC
nên BM=BC:2=32:2=16 (cm)
Xét ΔABM vuông tại M có:
AB2=AM2+BM2 (Định lý Py-ta-go)
nên 342=AM2+162
1156=AM2+256
AM2=1156-256
AM2=900
Vậy AM=30 (cm)
a. Xét ΔAMB và ΔAMC, ta có:
AM = AC (gt)
BM = CM (gt)
AM cạnh chung
Suy ra: ΔAMB = ΔAMC (c.c.c)
Suy ra: ∠(AMB) = ∠(AMC) (1)
Lại có: ∠(AMB) + ∠(AMC) = 180o (hai góc kề bù) (2)
Từ (1) và (2) suy ra: ∠(AMB) = ∠(AMC) = 90o
Vậy AM ⊥ BC.
b. Tam giác AMB có ∠(AMB) = 90o
Áp dụng định lí Pi-ta-go vào tam giác vuông AMB, ta có:
AB2 = AM2 + BM2 ⇒ AM2 = AB2 - BM2 = 342 - 162
= 1156 - 256 = 900
Suy ra: AM = 30 (cm).