Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài này cũng easy thôi!
A B C K H D O ( Chú ý: AO cắt BC ở D)
Gọi O là giao điểm hai đường cao(CK và BH)
=> O là trực tâm.
Mà AD đi qua O
=> AD là đường cao
Lại có : ΔABC cân tại A
=> AD là đường phân giác của \(\widehat{A}\)(dpcm)
CHÚC BAN HỌC TỐT!
A B C K H D
Xét \(\Delta ABH;\Delta ACK\) có :
\(\left\{{}\begin{matrix}AB=AC\\\widehat{AHB}=\widehat{AKC}\\\widehat{BAC}chung\end{matrix}\right.\)
\(\Leftrightarrow\Delta ABH=\Delta ACK\left(ch-gn\right)\)
\(\Leftrightarrow\widehat{ABH}=\widehat{ACK}\) và \(AH=AK\)
Ta có :
\(\left\{{}\begin{matrix}AH+HB=AB\\AK+KC=AC\end{matrix}\right.\)
Mà \(AB=AC;AH=AK\)
\(\Leftrightarrow HB=KC\)
Xét \(\Delta KDB;\Delta HDC\) có :
\(\left\{{}\begin{matrix}HB=KC\\\widehat{DHC}=\widehat{DKB}\\\widehat{DBK}=\widehat{DCH}\end{matrix}\right.\)
\(\Leftrightarrow\Delta KDB=\Delta HDB\left(g-c-g\right)\)
\(\Leftrightarrow KD=DH\)
Xét \(\Delta ADB;\Delta ADC\) có :
\(\left\{{}\begin{matrix}AH=AK\\\widehat{AKD}=\widehat{AHD}\\KD=DK\end{matrix}\right.\)
\(\Leftrightarrow\Delta ADB=\Delta AHC\left(c-g-c\right)\)
\(\Leftrightarrow\widehat{BAD}=\widehat{DAC}\)
Mà AD nằm giữa AB và AC
\(\Leftrightarrow AD\) là tia phân giác của \(\widehat{BAC}\)

Sai đề rồi phải là kẻ \(AH\perp BC\left(H\in BC\right)\) nhé!
A B C H E F
a) Xét 2 Δ vuông: Δ AHB = Δ AHC (c.h-g.n) vì:
\(\hept{\begin{cases}AB=AC\left(gt\right)\\\widehat{ACB}=\widehat{ABC}\left(gt\right)\end{cases}}\)
=> \(BH=HC\)
b) Xét 2 Δ vuông: Δ BHF = Δ CHE (c.h-g.n) vì:
\(\hept{\begin{cases}HB=HC\left(p.a\right)\\\widehat{HBF}=\widehat{HCE}\left(gt\right)\end{cases}}\)
=> \(HE=HF\) => Tam giác HEF cân tại H

Trả lời : Bn tham khảo link này :
https://h.vn/hoi-dap/question/559410.html
( Vào thống kê hỏi đáp của mk sẽ thấy )

A B C 5 5 8 H D E
Cm: Ta có: AB = AC <=> t/giác ABC là t/giác cân tại A
<=> góc B = góc C
Xét t/giác ABH và t/giác ACH
có góc BHA = góc CHA = 900 (gt)
AB = AC = 5 cm (gt)
góc B = góc C (cmt)
=> t/giác ABH = t/giác ACH (ch - gn)
=> BH = CH (hai cạnh tương ứng)
=> góc BAH = góc CAH (hai góc tương ứng)
b) Ta có: BH = CH = BC/2 = 8/2 = 4 (cm)
Xét t/giác ABH vuông tại H (áp dụng định lí Pi - ta- go)
=> AB2 = AH2 + BH2
=> AH2 = 52 - 42 = 9 = 32
=> AH = 3 (cm)
c) Xét t/giác ADH và t/giác AEH
có góc ADH = góc AEH = 900(gt)
AH : chung
góc DAH = góc EAH (cmt)
=> t/giác ADH = t/giác AEH (ch - gn)
=> HD = HE (hai cạnh tương ứng)
=> t/giác HDE là t/giác cân tại H

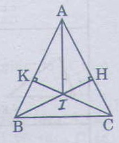
a) Hai tam giác vuông ABH và ACK có:
AB = AC(gt)
Góc A chung.
nên ∆ABH = ∆ACK(Cạnh huyền- Góc nhọn)
suy ra AH = AK.
b) Hai tam giác vuông AIK và AIH có:
AK = AH(cmt)
AI cạnh chung
Nên ∆AIK = ∆AIH(cạnh huyền- cạnh góc vuông)
Suy ra ˆIAKIAK^=ˆIAHIAH^
Vậy AI là tia phân giác của góc A.
a) Hai tam giác vuông ABH và ACH có:
Tam giác ABC cân tại A ⇒ AB = AC
AH cạnh chung.
Nên ∆ABH = ∆ACH(Cạnh huyền – cạnh góc vuông)
Suy ra HB = HC
b)∆ABH = ∆ACH (Câu a)
Suy ra ∠BAH = ∠CAH (Hai góc tương ứng)
A B C H K
MÌnh vẽ nhầm hình
Cho mình vẽ lại
A B C H K