Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
A B 2 = 6 2 = 36 A C 2 = 4 , 52 = 20 , 25 B C 2 = 7 , 52 = 56 , 25
Vì A B 2 + A C 2 = 36 + 20,25 = 56,25 = B C 2 nên tam giác ABC vuông tại A (theo định lí đảo Pi-ta-go)
Kẻ AH ⊥ BC
Ta có: AH.BC = AB.AC
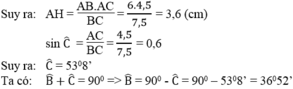
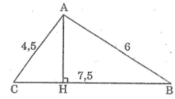

a) Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Xét ΔABC vuông tại A có
\(\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\)
nên \(\widehat{C}\simeq37^0\)
\(\Leftrightarrow\widehat{B}=53^0\)

Xét ΔABC có \(BC^2=BA^2+AC^2\)
nên ΔBAC vuông tại A
Xét ΔBAC có
BD là đường phân giác ứng với cạnh AC
nên \(\dfrac{AD}{AB}=\dfrac{DC}{BC}\)
hay \(\dfrac{AD}{4.5}=\dfrac{DC}{7.5}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{4.5}=\dfrac{DC}{7.5}=\dfrac{AD+DC}{4.5+7.5}=\dfrac{1}{2}\)
Do đó: AD=2,25cm; DC=3,75cm
Áp dụng định lí Pytago vào ΔABD vuông tại A, ta được:
\(BD^2=AD^2+AB^2\)
\(\Leftrightarrow BD^2=4.5^2+2.25^2=25.3125\)
hay \(BD=\dfrac{9\sqrt{5}}{4}\left(cm\right)\)
Xét ΔABD vuông tại A có
\(\sin\widehat{ABD}=\dfrac{AD}{BD}=\dfrac{\sqrt{5}}{5}\)
\(\cos\widehat{ABD}=\dfrac{AB}{BD}=\dfrac{2\sqrt{5}}{5}\)
\(\tan\widehat{ABD}=\dfrac{AD}{AB}=\dfrac{1}{2}\)
\(\cot\widehat{ABD}=2\)

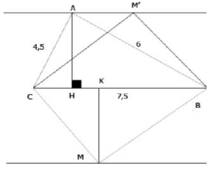
Ta có: AB2 + AC2 = 62 + 4,52 = 7,52 = BC2
nên tam giác ABC vuông tại A. (đpcm)
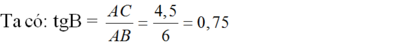
=> ∠B = 37o
=> ∠C = 90o - ∠B = 90o - 37o = 53o
Mặt khác trong tam giác ABC vuông tại A, ta có:
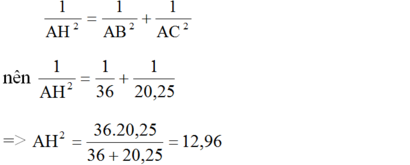
=> AH = 3,6 cm

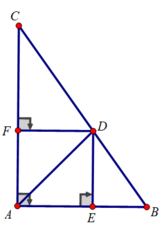
b) Do AD là tia phân giác của góc BAC, D ∈ BC nên ta có:
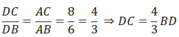
Mặt khác ta lại có:
DC + DB = BC ⇒ (4/3.BD) + BD = 10 ⇒ 7/3.BD = 10 ⇒ BD = 30/7 (cm)
Khi đó:
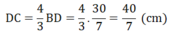

cho tam giác ABC vuông tại A .Biết AB=7cm và AC=21 cm .tính các tỉ số lượng giác của góc B vá góc C

Ta có:
7.5^2=4.5^2+6^2
→BC2=AB2+AC2
→ΔABC vuông tại A
Ta có BD là phân giác góc B→DA/DC=BA/BC=35
→DA/DA+DC=3/3+5
→AD/AC=38
→AD=3/8AC=94
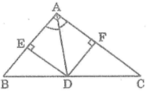

Ta có:
7.5^2=4.5^2+6^2
→BC2=AB2+AC2
→ΔABC vuông tại A
Ta có BD là phân giác góc B→DA/DC=BA/BC=35
→DA/DA+DC=3/3+5
→AD/AC=38
→AD=3/8AC=94
→BD=√AB2+AD2=9√54→BD=AB2+AD2=954
→sinˆABD=ADBD=1√5→sinABD^=ADBD=15
cosˆABD=ABBD=2√5cosABD^=ABBD=25
tanˆABD=sinˆABDcosˆABD=12tanABD^=sinABD^cosABD^=12
cotˆABD=1tanˆABD=2