
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


bn rảnh vc
thế giới tồn tại loại rảnh và xàm l như bn cx tốt :)
cảm ơn về chuyên mục của chúa PaiN nhá :))
ta đã tốn thời gian để share cách giải toán cho những thằng ngu như bạn ? bạn phải biết ơn chứ ?
nếu bạn biết rồi thì biến okay
\(1+1=?\) \(Ai\)\(k\)\(mk\)\(,mk\) \(k\)\(\)


Đây không phải toán lớp 1 đâu bạn
Tớ không biết vì tớ mới lớp 5
K mk nha
*Mio*
Tự đăng bài rồi tự làm luôn à bn .
Đây ko pk là Toán lớp nhá
Học tôt nhé bn
# MissyGirl #

giả sử ta chia được một số cho 0. Vậy:
"Khi ta chia một số cho 0, ta được kết quả là bao nhiêu?"
Ví dụ: Kết quả của phép tính 10 ?
Chúng ta có những sự tranh luận sau:
Nhìn vào phân số 1x và cho x nhỏ dần. Dễ thấy rằng khi x càng nhỏ thì phân số 1x càng lớn, vì vậy, ta gọi giá trị 10 là vô cực.
Toán học ký hiệu vô cực là ∞, vậy ta có kết quả của 10 là ∞.
Thoạt nhìn, tường chừng như vấn đề đã được giải quyết. Như vậy, ta có thể thấy rằng 20 tương đương với 2.10=2.∞=∞
Phép tính 2 nhân vô cực là vô cực là hoàn toàn hiển nhiên, đúng chứ ?
Nếu tôi có phép hợp giữa 2 tập vô cực, tôi sẽ có tập vô cực
Kết quả vô cực vẫn đúng với phép tính như 3.10;4.10 và nhiều nữa.
Nhưng một vấn đề xảy ra khi ta có phép tính 0.10
0 nhân cho bao nhiêu cũng bằng không, vì vậy ta có:
0.10=0.∞=0
Ôi, dễ quá, vấn đề giải quyết xong
Nhưng mặt khác, những quy luật của số học cho phép ta đơn giản
a.ba=b
Cho nên chúng ta phải có:
0.10=1
bằng cách đơn giản cho 0
Như vậy, với 2 phép tính khác nhau cho ra 2 kết quả khác nhau cùng một phép tính là 0.10
Đó là:
0.10=1
Và:
0.10=0
Ngoài ra, việc chia hết cho 0 còn dẫn đến nhiều kết quả sai như số i,e,0=1
Vấn đề ở đây là nếu ta công nhận việc chia một số cho số 0, thì ta không thể có kết quả
0.x=0;∀x
Và cả kết quả:
a.ba=b;∀a,b
Vì vậy, nếu phép tính 10 cho ra một giá trị, kể cả giá trị ∞, chúng ta vô tình tạo ra một mớ kết quả hỗn độn
Với tư cách là một nhà toán học, chúng ta có thể chọn quy luật mà chúng ta muốn, không phải tất cả sự lựa chọn nào cũng đều dấn đến những định lý, định đề. Quả thực như vậy, bạn có quyền tạo dựng một định lý rằng kết quả của 10 là ∞ nhưng bạn sẽ mất đi những quy luật rất hữu ích như a.ba=b
Với trường hợp vô cực này, ta có thể coi như giá trị đó không phải là con số, mà phụ thuộc vào khái niệm của những quy luật số học.
Như vậy ta có những kết luận sau:
- Đừng bao giờ chia một số cho 0
- Phân số 10 không tồn tại.
Người ta quy ước bất cứ số nào có muc bằng 0 thì số đó bằng 1
với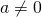 mà
mà 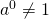 thì sẽ có mâu thuẫn
thì sẽ có mâu thuẫn
Thật vậy, giả sử rằng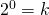 và
và 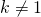 (*) khi đó một bài toán hết sức đơn giản sau đây sẽ có hai đáp số:
(*) khi đó một bài toán hết sức đơn giản sau đây sẽ có hai đáp số:
Tính giá trị của biểu thức
Là một bài toán hết sức đơn giản, đến mức quá tầm thường phải không, nhưng ta lại có thể giải nó theo 2 cách khác nhau với những đáp số khác nhau.
CÁCH 1: THỰC HIỆN PHÉP CHIA
Thực hiện một phép chia mà ai ai cũng biết. Thật là hiển nhiên, một số chia cho chính nó thì bằng 1 chứ còn bằng mấy? Vậy
Nhưng mặt khác:
CÁCH 2: ÁP DỤNG TÍNH CHẤT LŨY THỪA
Áp dụng tính chất của lũy thừa, ta có:
Theo giả sử ở trên thì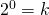 nên
nên
Từ (1)(2) ta có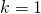 , mẫu thuẫn với giả thiết (*):
, mẫu thuẫn với giả thiết (*): 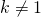 !! Sở dĩ có mâu thuẫn như thế là do ta đã giả sử
!! Sở dĩ có mâu thuẫn như thế là do ta đã giả sử 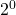 khác 1.
khác 1.
Như vậy, với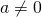 thì
thì 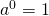 và có thể nói định nghĩa này nhằm để hợp lý hóa hay có nguồn gốc từ phép toán
và có thể nói định nghĩa này nhằm để hợp lý hóa hay có nguồn gốc từ phép toán 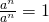 .
.
Đó nha
kb nhé
CHÚC BẠN HỌC TỐT!