Số học và cuộc sống
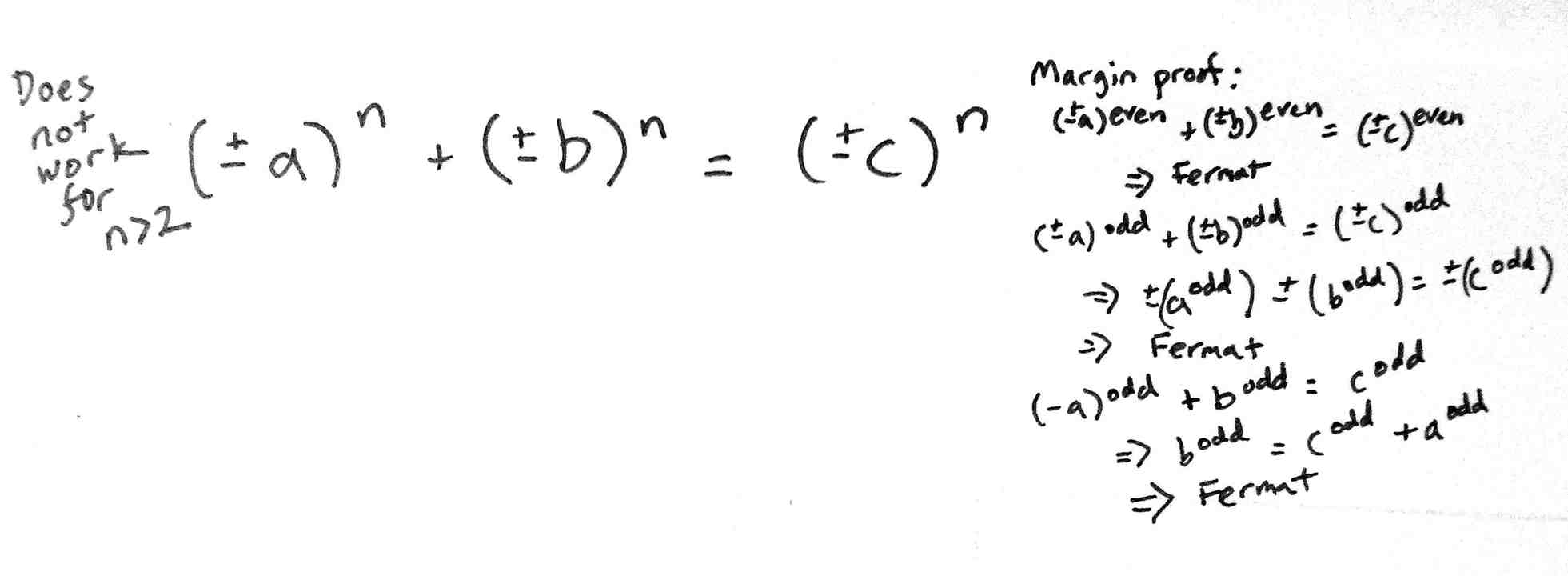
Ảnh không liên quan nhiều đến nội dung bài viết
Tất cả mọi sự so sánh đều khập khiễng, nhưng nếu sự so sánh kết nối được những thứ không liên quan với nhau thì đôi khi lại thật thú vị.
Cả ngày hôm nay tôi nghĩ về đúng một việc:
"8 với 9 cặp số gì ấy nhỉ?"
Nào, số 8 với số 9 không có gì đặc biệt, chỉ là hai số liền nhau trong tập N, chỉ là hai chữ số trong 10 chữ số đầu tiên, chỉ là một số lẻ và một số chẵn, chỉ là 2^3 và 3^2, ấy, chờ đã...
2^3 và 3^2 đúng không. nào:
3-2=1
3^2-2^3 = 1
Ồ, vậy nếu như chúng ta tổng quát hóa lên thì sao? Liệu chúng ta có những lũy thừa nguyên liên tiếp hay không?
Một trong những nhà toán học đại tài của nhân loại, Euler (1707-1783), đã nghĩ đến việc này, ông chứng minh được (8,9) là nghiệm duy nhất của phương trình Diophante (hay còn gọi là phương trình nghiệm nguyên):

Cách giải xin không trình bày ở đây, vì mục đích của bài viết này không phải giải toán
Nhưng Euler cũng chỉ có thể nghĩ được đến như vậy. Ông không tổng quát hóa bài toán này. Có điều, điểm đẹp đẽ của toán học nói chung, đó là sự tổng quát hóa. Thầy giáo toán của tôi từng nói rằng: Nếu như có một nhà toán học nào đó tìm được một ví dụ cụ thể nào đó, chắc chắn sẽ có một nhà toán học khác tổng quát hóa ví dụ đó. Phương trình trên của Euler không phải là ngoại lệ. Người tổng quát hóa phương trình của ông xuất hiện sau đó 100 năm, với cái tên Eugène Charles Catalan (1814 - 1894).
Và đó là lý do "Giả thuyết Catalan" ra đời. Giả thuyết này được trình bày như sau:
Phương trình Diophante
Không có nghiệm nào khác ngoài:
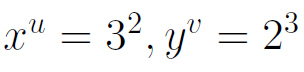
Một lần nữa, tôi sẽ không chứng minh bài toán này, mà thực tế thì tôi cũng không đủ trình độ để chứng minh nổi trường hợp tổng quát
Các bạn thử đoán xem mất bao nhiêu lâu thì giả thuyết này được chứng minh (với đơn vị là năm):
A. 100
B. 200
C. 300
D. 400
Mathematics is the queen of the sciences and number theory is the queen of mathematics.
Carl Friedrich Gauss
Tạm dịch: "Toán học là bà chúa của khoa học, và số học là bà chúa của toán học."
Và một trong những cuốn sách khiến tôi đam mê với toán học, cũng có tên "Số học - Bà chúa của toán học" của tác giả Hoàng Chúng

Cảm ơn bạn Trần Trung Đức, hồi đấy bạn học lớp 9 thì chắc là cũng tầm tuổi tôi giờ nên gọi "bạn" vậy
Tất nhiên, lúc ngấu nghiến quyển sách này trong ba tháng hè hồi phổ thông, thì tôi không nghĩ được là vì sao lại có câu nói đấy. Bởi vì thực ra mà nói, số học là môn học có ít "trọng lượng" nhất trong số các nhánh toán sơ cấp cũng như toán cao cấp. Tôi không quá rõ về toán cao cấp vì tôi chỉ học một ít trong đại học và không học lên nữa, nhưng đối với toán sơ cấp dạy trong phổ thông thì rất rõ ràng.
Mặc dù chương trình phổ thông lúc đó dạy số học đến lớp 9, nhưng chưa bao giờ bài toán số học trong các kỳ thi lại có điểm cao cả. Thường bài số học sẽ là bài "khó nhất" và chỉ có 1 điểm. Điều này đúng với mọi kỳ thi, từ thi học kỳ, đến thi học sinh giỏi các cấp, thậm chí là cả đối với các kỳ thi quốc tế. Thế nếu như không được chú trọng như vậy, tại sao số học vẫn được mệnh danh là "Bà chúa của toán học"?
Tôi biết được câu trả lời khi tôi bỏ không theo toán được gần chục năm. Đôi khi nghĩ lại thì đó là một tình huống tréo ngoe đi kèm với nực cười.
Bây giờ hãy nghĩ thử nhé. Chúng ta đi học lớp 1 được dạy 1+1 = 2, một hai năm sau thì biết 2x2=4, một vài năm nữa thì biết 4^4=256, thêm một vài năm nữa thì số 256 này biến đi đâu mất để chỉ còn toàn x với y, đôi khi là zigma và pi rồi hàng loạt những ký hiệu cổ quái. Rất nhiều người trong số chúng ta sẽ cảm thấy chán nản với zigma và pi, cảm thấy tại sao trước kia 1+1 = 2 vui thế mà giờ chứng minh mấy cái bất đẳng thức chẳng có số má gì chán bỏ mẹ (xin lỗi nói bậy), rồi ngáp ngắn ngáp dài trên đống ký hiệu với câu hỏi hiện sinh: Mình học những thứ này để làm gì cho cuộc đời?
Cho đến một ngày tôi nhận ra là tất cả những thứ quan niệm đấy đều sai lầm, bởi tư duy toán học, tư duy số học là thứ trân quý nhất mà cuộc đời này có thể dạy cho tôi.
Toán học không phải là về những con tính, không phải là về những định lý, những giả thuyết, mà nó chính là về mối quan hệ giữa những yếu tố trong đó. Mà rồi số học, lại thể hiện những mối quan hệ đó một cách nguyên sơ, trần trụi nhất, bằng những thứ tưởng chừng như đơn giản nhất, không đáng quan tâm nhất.
Chúng ta ngẫu nhiên chấp nhận những con số 1, 2, 3... trong cuộc đời, chúng ta ngẫu nhiên chấp nhận những phép tính +, -, x, / trong cuộc đời. Nếu đứng riêng rẽ ra, chúng chẳng là gì cả, nhưng khi chúng ta ghép nối chúng lại, không biết bao nhiêu vấn đề nảy sinh ra.
Cái ngày mà Pythagoras phát hiện ra rằng:
3x3 + 4x4 = 5x5
Là cái ngày mà nhân loại này có một bước tiến vĩ đại.
Cái ngày mà Fibonacci đem cộng thử mấy con số vào với nhau để tạo thành dãy:
1, 1, 2, 3, 5, 8...
Là cái ngày khiến cho vài trăm năm sau không biết bao nhiêu tay chơi poker mà biết phải thầm cảm ơn.
Cái ngày mà Euclid chứng minh rằng dãy số nguyên tố vô hạn:
2, 3, 5, 7, 11, 13, 17, 19, 23...
Là cái ngày cũng khiến cho vài trăm năm sau trường đại học mật mã ở Việt Nam vẫn có người học (đùa đấy).
Số học được xây dựng trên nền tảng của những thứ cơ bản và thuần túy nhất của toán học như thế. Rồi số học lại dạy ta rằng, nếu chúng ta tổng quát hóa những thứ cơ bản và thuần tý đấy lên, con đường phía trước mặt chúng ta là vô hạn lượng. Đó là lý do vì sao số học lại là bà chúa của toán học, bởi nếu không có phương pháp tư duy của số học, toán học không thể phát triển, và từ đó dẫn đến khoa học không thể phát triển.
Đây cũng là thứ nguyên lý khiến con người như một giống loài phát triển, và là thứ nguyên lý khiến con người như một cá thể phát triển.
Cuộc sống vận động với một dạng nguyên lý của riêng nó. Nhưng nếu như chúng ta áp dụng thứ tư duy số học từ cụ thể đến tổng quát (không phải trừu tượng, trừu tượng là phạm trù khác), có rất nhiều lúc chúng ta sẽ thấy rằng mọi thứ đều có thể có sự liên quan đến nhau. Mọi yếu tố đều xuất phát từ đâu đó, giống như mọi số nguyên đều có thể phân tích thành tích các số nguyên tố (ngoại trừ chính các số nguyên tố - thành phần cá biệt điển hình); mọi yếu tố đều có liên kết với nhau, chỉ là chúng ta có tìm tòi được đến cái liên kết đấy hay không; rồi khi tìm được liên kết đấy rồi, chúng ta có đủ khả năng trong cuộc đời chúng ta để tổng quát hóa lên hay không?
Khi bạn tìm được càng nhiều sự liên kết, thế giới quan của bạn càng rộng. Mà về mặt này, những người có năng khiếu về toán, thiên vị và tự hào hơn một chút (xin lỗi) là năng khiếu về số học đi chẳng hạn (thường đi cùng với một đam mê về toán theo cách này hay cách khác) lại có lợi thế hơn những người khác. Mặt trái là đôi khi họ mải mê tìm kiếm những thứ liên kết quá, mải mê tổng quát hóa quá mà quên mất rằng cuộc đời mình vốn hữu hạn trên cái hành trình vô hạn đấy. Hoặc cũng có thể họ mải mê tìm kiếm những thứ nhân tố nhỏ nhất quá mà bị chìm đắm trong cái thế giới của riêng mình.
Lúc mới đi làm, khi nộp hồ sơ xin việc, rất nhiều người ngạc nhiên rằng tôi học chuyên về toán mà rồi lại làm những công việc toàn có liên quan đến viết lách, sản xuất nội dung, tôi chỉ cười thầm mà nghĩ rằng đó là vì họ không bao giờ đủ tò mò để tìm kiếm sự liên kết giữa những thứ như thế. Còn tôi, khi tìm được sự liên kết đấy thì lại thấy nó thú vị đến mức hoàn toàn chẳng còn theo đuổi ngành toán nữa. Nhưng đôi khi tôi vẫn cảm ơn thứ tư duy được rèn giũa trước kia, bởi nhờ nó mà tôi biết mình ở đâu, biết mình làm được cái gì, hiểu được những người tôi tiếp xúc đang ở đâu, hiểu được họ làm được cái gì, hiểu được xã hội xung quanh tôi đang ở đâu, hiểu được xã hội xung quanh tôi làm được cái gì. Chỉ cần thế thôi, chứ cũng chẳng cần phải hiểu thế giới này đang ở đâu và làm được cái gì. Việc đấy, chỉ đơn thuần về mặt lý thuyết, đã là không thể rời xa


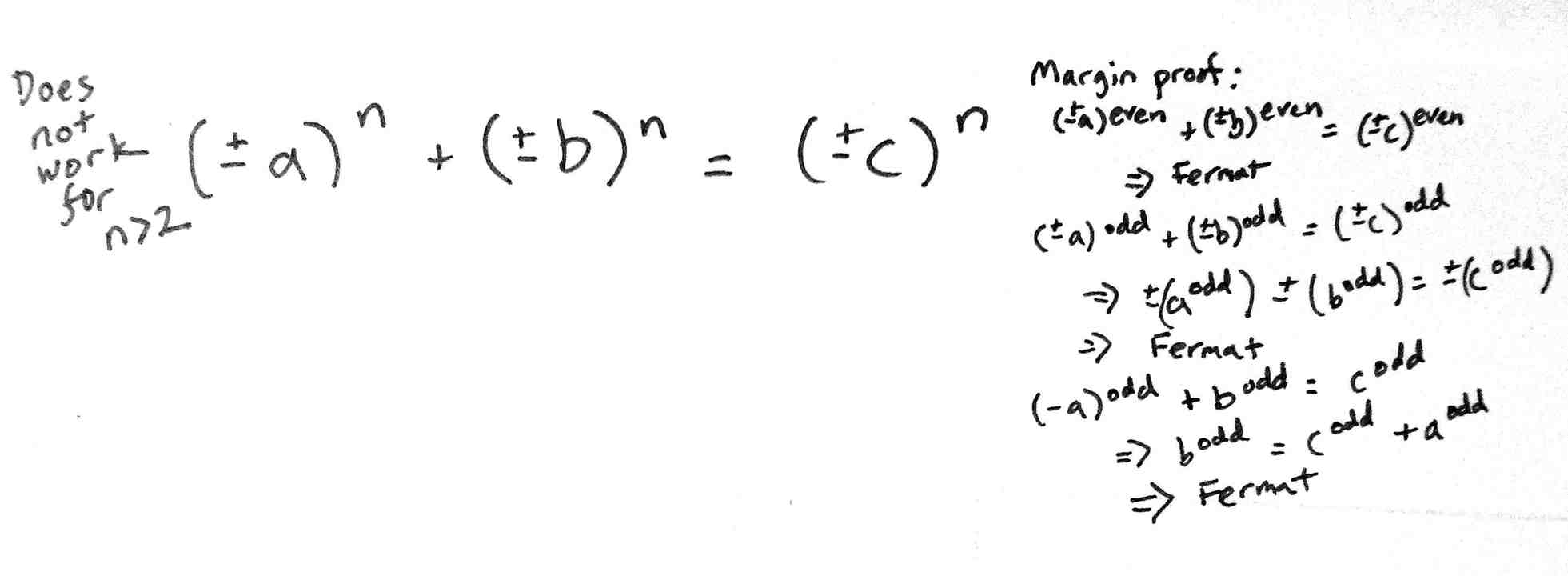

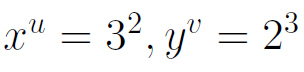

Số nguyên tố là số chỉ có 2 ước là 1 và chính nó, tức là nó chỉ chia hết cho 1 và chính nó. Trong các số nguyên tố , chỉ có số 5 chia hết cho 1 và cho 5, các số lớn hơn 5 hay khác 5 đều không chia hết cho 5 , vậy nó chia 5 dư 1,2,3,4 => số nguyên tố p >5 có dạng 5k,5k+1,5k+2,5k+3,5k+4 (k thuộc N)
cảm ơn bạn nha cô giáo dạy rồi mà tớ quên mất