Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp:
Áp dụng lí thuyết về giao thoa sóng ánh sáng, công thức tính khoảng vân i = λD/a
Cách giải:
+ Khi chưa dịch màn M:

+ Khi dịch màn M ra xa một đoạn 40 cm:
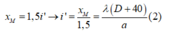
Từ (1) và (2) ta có:
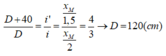
+ Khi dịch màn M lại gần một đoạn 40 cm:
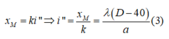
Từ (1) và (3) ta có:
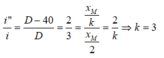
Vậy tại M có vân sáng bậc 3
Chọn A

+ Vì khi M ở vị trí cao nhất hoặc thấp nhất thì N ở vị trí cân bằng nên dao động tại hai điểm này là vuông pha với nhau.
→ Độ lệch pha giữa hai điểm đó là số lẻ lần π 2 .
Đáp án C

+ Vì khi M ở vị trí cao nhất hoặc thấp nhất thì N ở vị trí cân bằng nên dao động tại hai điểm này là vuông pha với nhau.
® Độ lệch pha giữa hai điểm đó là số lẻ lần π 2
Chọn đáp án C

- Vì khi M ở vị trí cao nhất hoặc thấp nhất thì N ở vị trí cân bằng nên dao động tại hai điểm này là vuông pha với nhau.
→ Độ lệch pha giữa hai điểm đó là số lẻ lần π/2

Chọn C

+ Độ giảm biên độ trong nửa chu kì: ![]()
+ Theo yêu cầu của đề: 0,04 + (0,04 – ΔA) < S < 0,04 + 2(0,04 – ΔA)
=> 0,08 – 0,4μ < S < 0,12 – 0,8μ
+ Tới khi dừng hẳn: ![]()
+ 0,08 – 0,4μ < 4.10-3 /μ => (μ – 0,1)2 > 0
+ 4.10-3 /μ < 0,12 – 0,8μ => μ2 – 0,15μ + 0,005 < 0 => 0,05 < μ < 0,1.

Ta có OM=5.25mm
ở vị trí đầu tiên M trùng vơi vị trí vân sáng số 5 nên
\(i_1=\frac{OM}{5}=1,05mm\)
Lúc sau thì M ứng với vị trí vân tối lần thứ 2( chính là vân tối thứ 4, lần 1 qua vị trí 4.5i' lần thứ 2 qua vị trí 3.5i'')
\(i_2=\frac{OM}{3,5}=1,5mm\)
Mặt khác \(i=\frac{D\lambda}{a}\)
\(\frac{i_1}{i_2}=\frac{D_1}{D_2}=\frac{7}{10}\)
\(D_2-D_1=0,75m\)
\(D_1=1,75m\)
\(\lambda=\frac{i_1a}{D_1}=0,6\mu m\)