K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HT
3
HP
6 tháng 5 2021
47.
\(\left(cot\alpha+tan\alpha\right)^2=\left(\dfrac{cos\alpha}{sin\alpha}+\dfrac{sin\alpha}{cos\alpha}\right)^2=\left(\dfrac{cos^2\alpha+sin^2\alpha}{sin\alpha.cos\alpha}\right)^2=\dfrac{1}{sin^2\alpha.cos^2\alpha}\)
6 tháng 5 2021
(cota +tana)\(^2\)=cot\(^2\)a+2cota.tana+tan\(^2\)a=(cot\(^2\)a +1)+(tan\(^2\)+1)=\(\dfrac{1}{sin^2a}\)+\(\dfrac{1}{cos^2a}\)=\(\dfrac{cos^2a+sin^2a}{cos^2a.sin^2a}\)=\(\dfrac{1}{cos^2a.sin^2a}\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 5 2021
8.
\(0< a< \dfrac{\pi}{2}\Rightarrow cosa>0\Rightarrow cosa=\sqrt{1-sin^2a}=\dfrac{2\sqrt{2}}{3}\)
\(cosa-sina=\dfrac{2\sqrt{2}}{3}-\dfrac{1}{3}=\dfrac{-1+2\sqrt{2}}{3}\)
9.
Có 2 điểm (ứng với \(k=0\) và \(k=1\))
10.
\(2-x\ge0\Leftrightarrow x\le2\)
\(\Rightarrow S=(-\infty;2]\)
11.
Phương trình AB theo đoạn chắn: \(\dfrac{x}{3}+\dfrac{y}{-4}=1\Leftrightarrow\dfrac{x}{3}-\dfrac{y}{4}=1\)
10 tháng 3 2022
Câu 93
Ta có \(AC^2=AB^2+BC^2-2.AB.BC.cosB=19\Rightarrow AC=\sqrt{19}\)
chọn D
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 12 2021
\(5\overrightarrow{v}=3\overrightarrow{b}-2\overrightarrow{a}\Rightarrow\overrightarrow{v}=\dfrac{3}{5}\overrightarrow{b}-\dfrac{2}{5}\overrightarrow{a}=\dfrac{3}{5}\left(-1;2\right)-\dfrac{2}{5}\left(3;-4\right)=\left(-\dfrac{9}{5};\dfrac{14}{5}\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 3 2022
\(sina.sinb=-\dfrac{1}{2}\left[cos\left(a+b\right)-cos\left(a-b\right)\right]\) là công thức đúng
AH
Akai Haruma
Giáo viên
25 tháng 10 2021
Lời giải:
a. TXĐ: $\mathbb{R}$
Với $x\in\mathbb{R}$ thì $-x\in\mathbb{R}$
$f(x)=|x|=|-x|=f(-x)$
$\Rightarrow $ hàm chẵn
b. TXĐ: $\mathbb{R}$
Với $1\in\mathbb{R}$ thì $-1\in\mathbb{R}$
$f(1)=9; -f(1)=-9; f(-1)=1$
$\Rightarrow f(1)\neq f(-1); -f(1)\neq f(-1)$ nên hàm không chẵn không lẻ.
c.
TXĐ: $\mathbb{R}$
Với $x\in\mathbb{R}$ thì $-x\in\mathbb{R}$
$f(-x)=(-x)^3+(-x)=-(x^3+x)=-f(x)$ nên hàm lẻ
d.
TXĐ: $\mathbb{R}$
Với $1\in\mathbb{R}$ thì $-1\in\mathbb{R}$
$f(1)=3; f(-1)=1$
$\Rightarrow f(1)\neq f(-1); -f(1)\neq f(-1)$
Do đó hàm không chẵn không lẻ.
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 4 2021
11.
\(BPT\Leftrightarrow\left\{{}\begin{matrix}3-x>0\\\left|1-x\right|>x-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x< 3\\\left|x-1\right|>x-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x< 3\\x-1< 0\end{matrix}\right.\) \(\Leftrightarrow x< 1\)
Đáp án A
12.
Đường thằng d nhận (1;2) là 1 vtpt nên đường thẳng vuông góc d nhận (2;-1) là 1 vtpt
\(\Rightarrow\) Loại A, C
Với đáp án B, đường thẳng cắt 2 trục tại \(A\left(0;-1\right)\) và \(B\left(\dfrac{1}{2};0\right)\)
\(S_{OAB}=\dfrac{1}{2}.1.\left(\dfrac{1}{2}\right)=\dfrac{1}{4}\ne1\) (ktm)
Vậy D là đáp án đúng
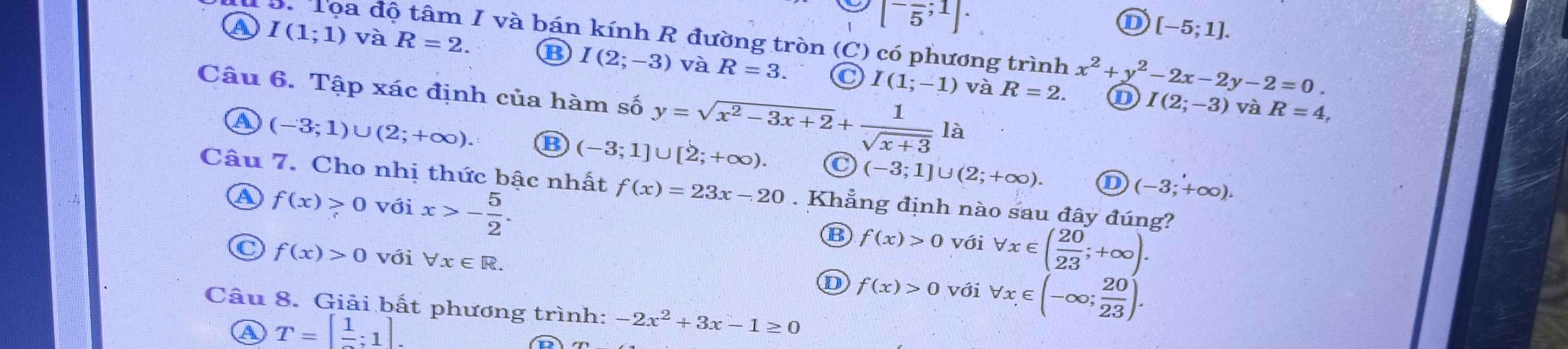
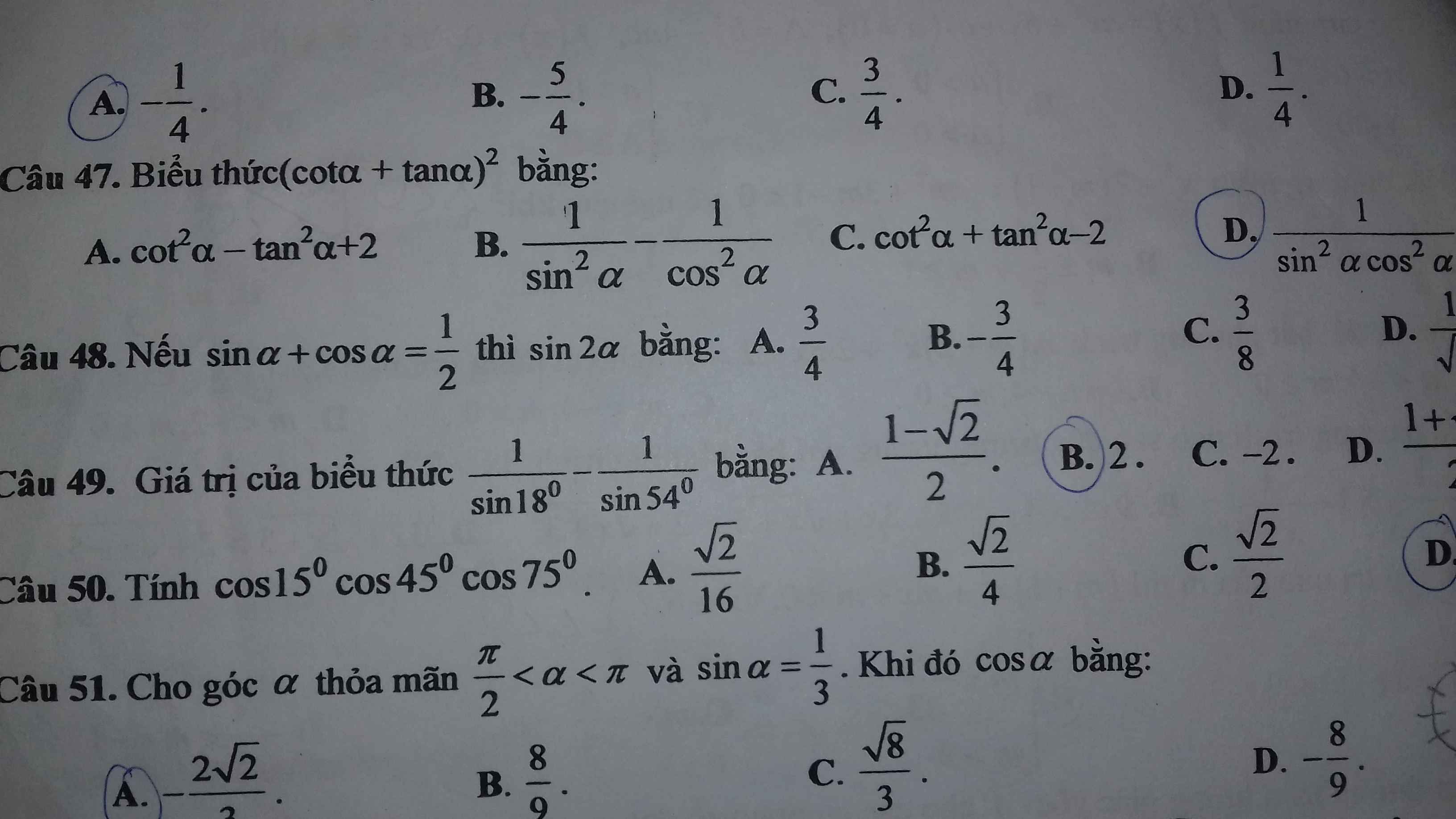
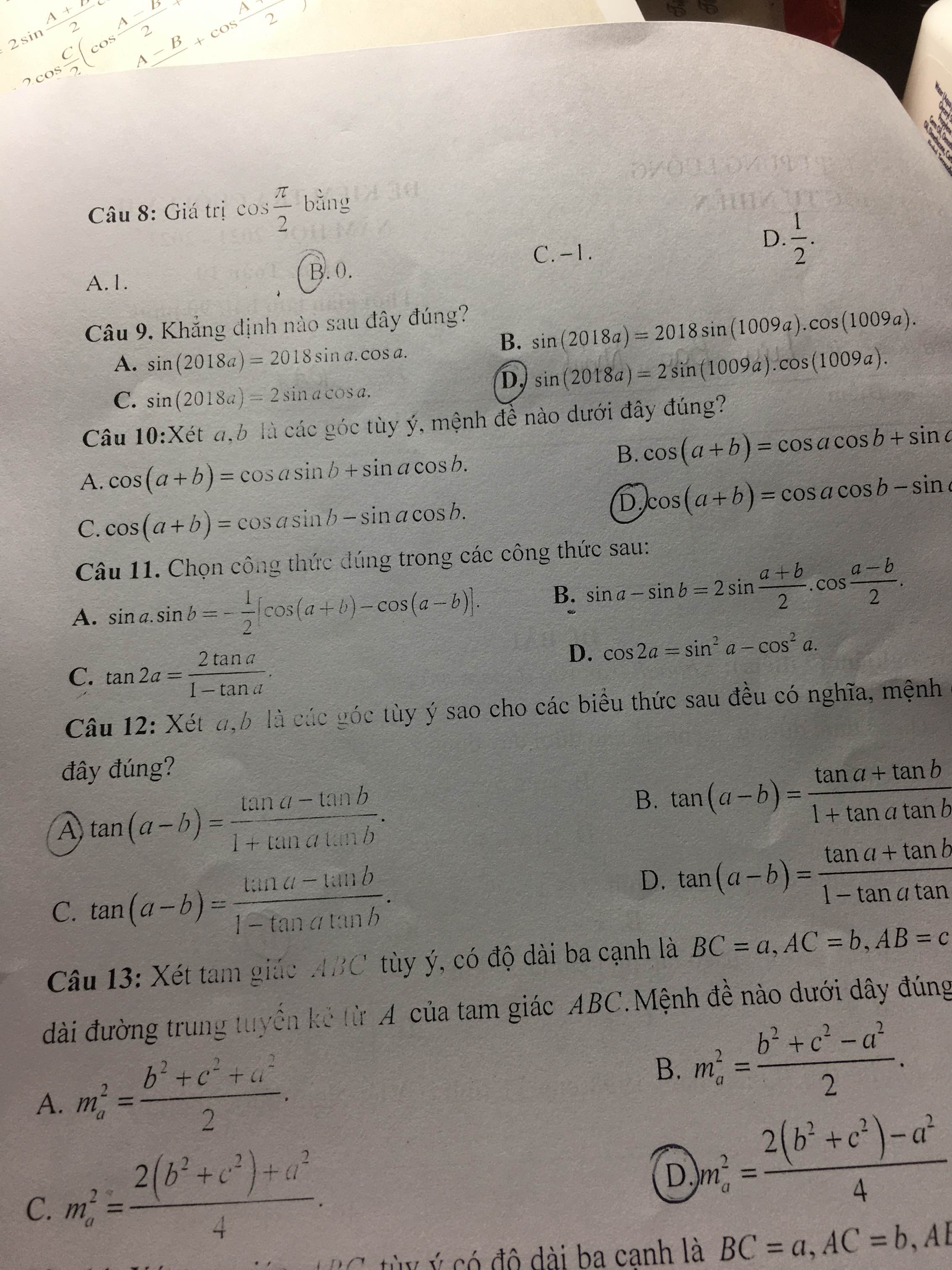
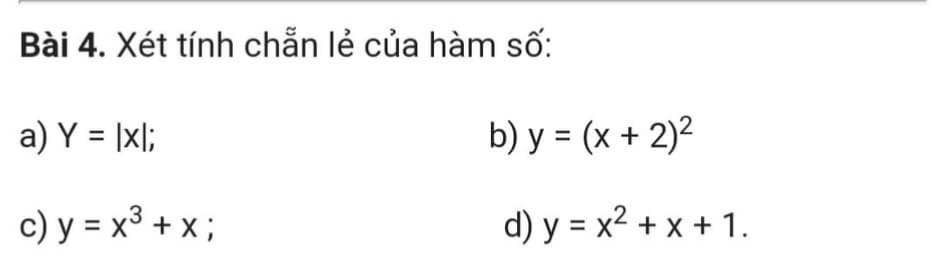
Câu 11:
Gọi pt là y=ax+b
=> 3a+b=-7; a+b=-7
<=>a=0; b=-7
=> y=-7 -> (b)
Câu 11 đáp án là D chứ bạn, sao lại B