Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B
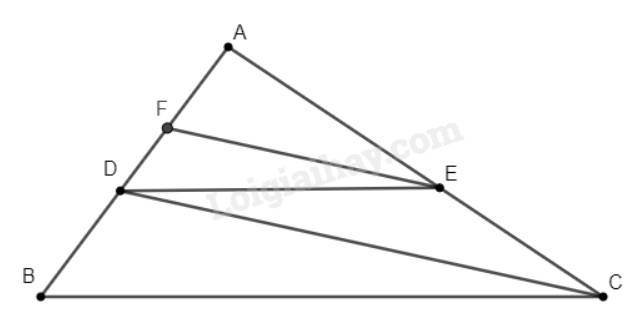
Xét tam giác \(ADC\) có \(EF//DC\), theo định lí Thales ta có:
\(\frac{{AF}}{{AD}} = \frac{{AE}}{{AC}}\) (1)
Xét tam giác \(ABC\) có \(DE//BC\), theo định lí Thales ta có:
\(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}\) (2)
Từ (1) và (2) suy ra,
\(\frac{{AF}}{{AD}} = \frac{{AD}}{{AB}} \Rightarrow AF.AB = A{D^2} \Leftrightarrow 9.25 = A{D^2} \Rightarrow AD = \sqrt {9.25} = 15\)
Xét tam giác \(ADC\) có \(EF//DC\), theo hệ quả định lí Thales ta có:
\(\frac{{AF}}{{AD}} = \frac{{EF}}{{DC}} \Rightarrow \frac{9}{{15}} = \frac{{12}}{{DC}} \Leftrightarrow DC = \frac{{12.15}}{9} = 20\)
Vậy \(DC = 20cm\).

I A B D C E F K
Gọi I là trung điểm của AB.
Giả sử đường thẳng IE cắt CD tại K1
Có: \(\frac{IA}{K_1D}=\frac{EI}{EK_1}=\frac{IB}{K_1C}\) (hệ quả định lý Ta lét)
mà IA = IB (gt) nên K1D = K1C, do đó K1 là trung điểm CD
Giả sử đường thẳng IF cắt CD tại K2
Có: \(\frac{IA}{K_2C}=\frac{FI}{FK_2}=\frac{IB}{K_2D}\) (hệ quả định lý Ta lét)
mà IA = IB (gt) nên K2C = K2D, do đó K2 là trung điểm CD
do IE và IF cùng đi qua trung điểm K của CD nên hai đường thẳng này trùng nhau
Vậy ta có đpcm

Hình thang ABCD (AB//CD) có: M là trung điểm AE, MN//AB//EF.
\(\Rightarrow\)N là trung điểm BF nên MN là đường trung bình của hình thang ABCD.
\(\Rightarrow MN=\dfrac{AB+EF}{2}=\dfrac{12+18}{2}=15\left(cm\right)\).
Hình thang MNCD (MN//CD) có: E là trung điểm MD, EF//MN//CD.
\(\Rightarrow\)F là trung điểm CD nên EF là đường trung bình của hình thang MNCD.
\(\Rightarrow EF=\dfrac{MN+CD}{2}\Rightarrow CD=2EF-MN=2.18-15=21\left(cm\right)\)