Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)\(\left(-a+\frac{2}{3}\right)\left(a+\frac{2}{3}\right)=\left(\frac{2}{3}-a\right)\left(\frac{2}{3}+a\right)=\left(\frac{2}{3}\right)^2-a^2=\frac{4}{9}-a^2\)
b)\(\left(x+5\right)\left(x^2-5x+25\right)=x^3+5^3=x^3+125\)
c)\(\left(1-x\right)\left(x^2+x+1\right)=1-x^3\)
d)\(\left(a^2-2a+3\right)\left(a^2+2a+3\right)=\left(a^2+3\right)^2-\left(2a\right)^2=\left(a^2+3\right)^2-4a^2\)
e)\(\left(x+3y\right)\left(9y^2-3xy+x^2\right)=x^3+\left(3y\right)^3=x^3+9y^3\)
f)\(2\left(x-\frac{1}{2}\right)\left(4x^2+2x+1\right)=\left(2x-1\right)\left(4x^2+2x+1\right)=\left(2x\right)^3-1=8x^3-1\)

Trả lời:
Bài 1:
a, \(9x^2-4=\left(3x\right)^2-2^2=\left(3x-2\right)\left(3x+2\right)\)
b, \(x^3+27=x^3+3^3=\left(x+3\right)\left(x^2-3x+9\right)\)
c, \(8-y^3=2^3-y^3=\left(2-y\right)\left(4+2y+y^2\right)\)
d, \(x^4-81=\left(x^2\right)^2-9^2=\left(x^2-9\right)\left(x^2+9\right)\)\(=\left(x^2-3^2\right)\left(x^2+9\right)=\left(x-3\right)\left(x+3\right)\left(x^2+9\right)\)
e, \(64x^3-1=\left(4x\right)^3-1^3=\left(4x-1\right)\left(16x^2+4x+1\right)\)
f, \(x^6+8y^3=\left(x^2\right)^3+\left(2y\right)^3=\left(x^2+2y\right)\left(x^4-2x^2y+4y^2\right)\)

Tam giác ABC vuông tại A có AM là trung tuyến ứng với cạnh huyền
\(\Rightarrow AM=\dfrac{1}{2}BC\Rightarrow BC=2AM=50\left(m\right)\)
a. Áp dụng định lý Pitago:
\(AB=\sqrt{BC^2-AC^2}=30\left(m\right)\)
b. Kẻ \(MH\perp AC\Rightarrow MH||AB\) (cùng vuông góc AC)
Mà M là trung điểm BC \(\Rightarrow MH\) là đường trung bình tam giác ABC
\(\Rightarrow MH=\dfrac{1}{2}AB=15\left(m\right)\)
\(\Rightarrow S_{AMC}=\dfrac{1}{2}MH.AC=\dfrac{1}{2}.15.40=300\left(m^2\right)\)

1) Gọi số bé là x
Số lớn là 12 + x
Chia số bé cho 7 có thương là \(\frac{x}{7}\)
Chia số lớn cho 5 có thương là: \(\frac{12+x}{5}\)
Theo bài ra ta có: \(\frac{12+x}{5}-\frac{x}{7}=4\)
<=> \(\frac{x}{5}-\frac{x}{7}=4-\frac{12}{5}\)
<=> \(\frac{2}{35}x=\frac{8}{5}\)
<=> \(x=28\)
Vậy hai số đó là 28 và 28 + 12 = 40.

| Vt | Tgian | Q.duong | |
| luc di | 45 | x | 45x |
| luc ve | 60 | x-50 | 60(x-50) |
ta co ph trinh
45x=60(x-50)
x=200 km
cho mk cai h nha

Bài 1.
Gọi số cần tìm là ab ( \(0< a\le9,0\le b\le9\))
Viết thêm chữ số 5 vào bên trái ta được số A
=> A = 5ab
Viết thêm chữ số 5 vào bên phải tâ được số B
=> B = ab5
Theo đề bài ta có : A - B = 153
<=> 5ab - ab5 = 153
<=> 500 + ab - ( ab.10 + 5 ) = 153
<=> 500 + ab - 10ab - 5 = 153
<=> 495 - 9ab = 153
<=> 9ab = 342
<=> ab = 38 ( tmđk )
Vậy số cần tìm là 38
Bài 2.
Gọi độ dài cạnh hình vuông đó là x ( m, x > 0 )
Tăng độ dài cạnh lên 12m => Độ dài mới = x + 12m
Diện tích ban đầu = x2 ( m2 )
Diện tích sau khi tăng = ( x + 12 )2 ( m2 )
Khi đó diện tích tăng 135m2
=> Ta có phương trình : x2 + 135 = ( x + 12 )2
<=> x2 + 135 = x2 + 24x + 144
<=> x2 - x2 - 24x = 144 - 135
<=> -24x = 9
<=> x = -9/24 = -3/8 ( Đến chỗ này nên xem lại đề )
Bài 3.
Gọi độ dài quãng đường AB là x ( km , x > 0 )
Thời gian người đó đi từ A đến B = x/25 ( giờ )
Thời gian người đó đi từ B về A = x/30 ( giờ )
Thời gian lúc về ít hơn thời gian lúc đi 20 phút = 1/3 giờ
=> Ta có phương trình : x/25 - x/30 = 1/3
<=> x( 1/25 - 1/30 ) = 1/3
<=> x . 1/150 = 1/3
<=> x = 50 ( tmđk )
Vậy quãng đường AB dài 50km
 đg cần gấp lúc 5h
đg cần gấp lúc 5h  lúc 5h
lúc 5h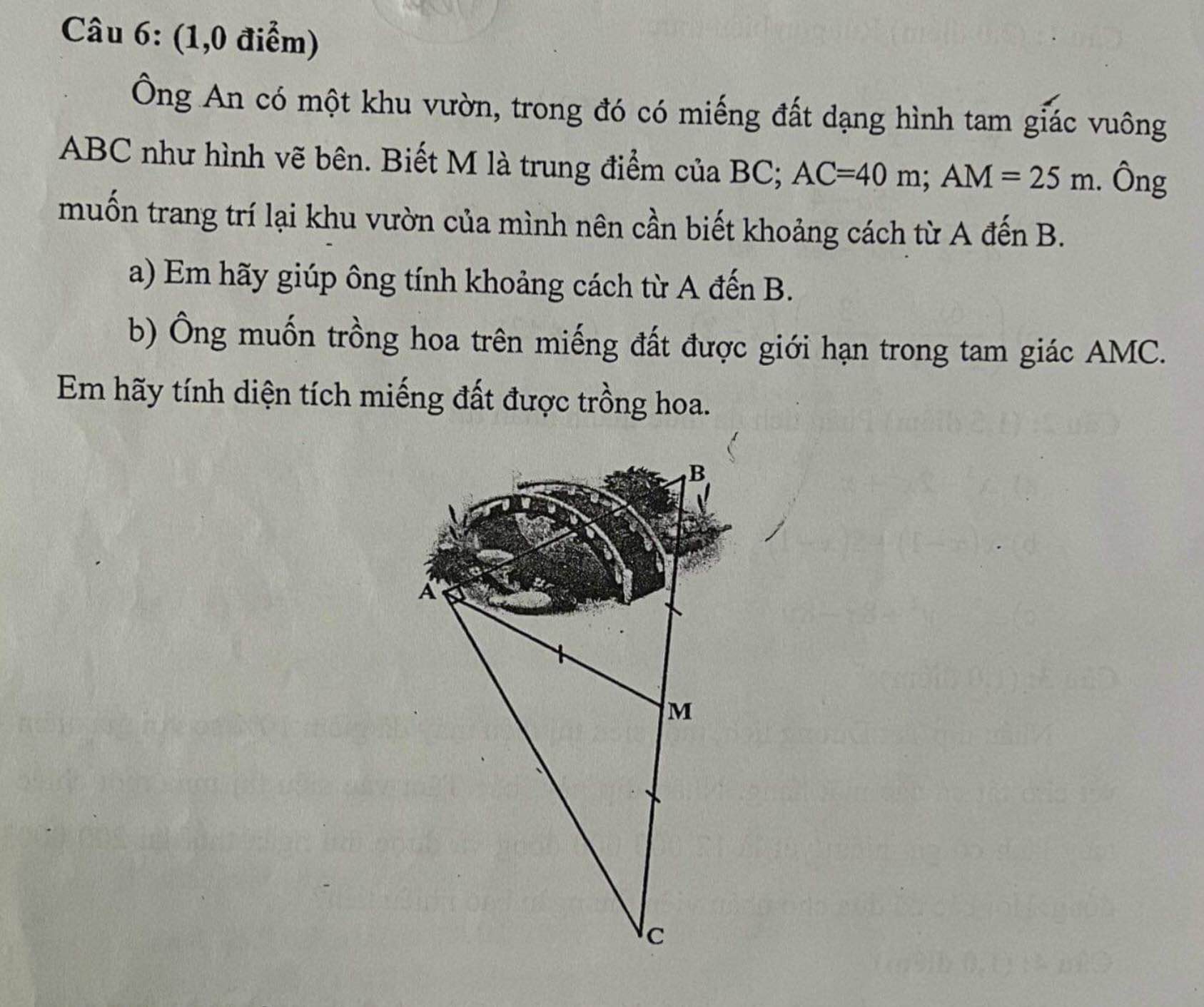
m.n vào giúp vs ạ