K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
18 tháng 7 2019
Đáp án D
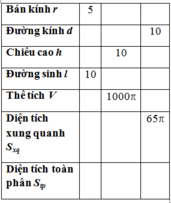
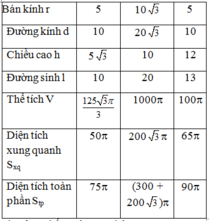
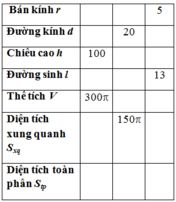
Diện tích hai đáy của hình trụ là: S d = 2 π r 2 = 8 π
Diện tích toàn phần của hình trụ là: S t p = 100 π + 8 π = 108 π
NK
0
PD
0
AH
Akai Haruma
Giáo viên
5 tháng 5 2020
Làm nốt bài 2 nhé. Hôm qua mình bận nên không làm tiếp được
Bài 2:
a) 4 điểm $C,M,B,N$ cùng thuộc $(O)$ nên $CNBM$ là tứ giác nội tiếp.
$\Rightarrow HC.HB=HM.HN$ (đây là tính chất quen thuộc)
Nếu muốn chứng minh chi tiết bạn có thể chỉ ra $\triangle HMB\sim \triangle HCN$ (g.g)
$\Rightarrow \frac{HM}{HC}=\frac{HB}{HN}\Rightarrow HM.HN=HB.HC$
b)
Vì $AC=AB$ (tính chất 2 tiếp tuyến cắt nhau tại 1 điểm). $OB=OC=R$ nên $OA$ là trung trực của $BC$
$\Rightarrow OA\perp BC$ tại $H$ và $H$ là trung điểm của $BC$. Từ đây ta có:
Tam giác $ACO$ vuông tại $C$, có $CH\perp AO$, áp dụng công thức hệ thức lượng trong tam giác vuông thì:
$HA.HO=CH^2$.
Mà $CH=BH$ (do $H$ là trung điểm của $BC$) nên $HA.HO=HC.HB$
Kết hợp với kết quả phần a suy ra $HA.HO=HM.HN$
$\Rightarrow \triangle AMON$ nội tiếp
$\Rightarrow \widehat{NAO}=\widehat{NMO}$ và $\widehat{MAO}=\widehat{MNO}$
Mà $\widehat{NMO}=\widehat{MNO}$ (do tam giác $MON$ cân tại $O$)
$\Rightarrow \widehat{NAO}=\widehat{MAO}(1)$
Mặt khác, cũng theo tính chất 2 tiếp tuyến cắt nhau tại 1 điểm, $AO$ là phân giác $\widehat{CAB}$ nên $\widehat{CAO}=\widehat{BAO}(2)$
Lấy $(2)-(1)$ suy ra $\widehat{CAN}=\widehat{MAB}$ (đpcm)
CM
1 tháng 1 2019
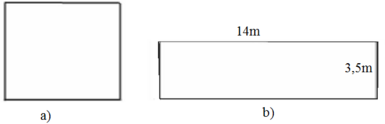
Diện tích hình chữ nhật: SHCN = 3 , 5 . 14 = 49 ( m 2 )
Gọi a (m) (a > 0) là độ dài của cạnh hình vuông. Suy ra diện tích hình vuông là
S H V = a 2 = 49 ( m 2 )
= > a = 7 ( m )
Vậy cạnh hình vuông có độ dài là 7m.
Ghi chú: Nếu ta cắt đôi hình chữ nhật thành hai hình chữ nhật có kích thước 3,5m x 7m thì ta sẽ ghép được hình vuông có cạnh là 7m.