Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có phải đề là: \(\left(\frac{a+b+c}{b+c+d}\right)^3=\frac{a}{d}?????????\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=\frac{a+b+c}{b+c+d}\)
Đặt: \(\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=\frac{a+b+c}{b+c+d}=t\) ta có:
\(\hept{\begin{cases}\left(\frac{a+b+c}{b+c+d}\right)^3=t^3\\\frac{a}{b}.\frac{b}{c}.\frac{c}{d}=\frac{a}{d}=t.t.t=t^3\end{cases}}\Rightarrowđpcm\)

Giải tương tự như bài tập 59
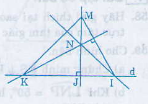
∆MKI có JM là đường cao (l ⊥ d), đường thẳng KN cũng là đường cao ( giả thiết KN ⊥ MI). Hai đường cao cắt nhau tại N nên N là trực tâm ∆MKI. Vậy NI ⊥ MK
Hướng dẫn:
Giải tương tự như bài tập 59

∆MKI có JM là đường cao (l ⊥ d), đường thẳng KN cũng là đường cao ( giả thiết KN ⊥ MI). Hai đường cao cắt nhau tại N nên N là trực tâm ∆MKI. Vậy NI ⊥ MK

x O z y t m
a, Ta có : góc yOz = góc xOz - góc xOy
\(\Rightarrow\) góc yOz = 120độ - 50độ
\(\Rightarrow\) góc yOz = 70độ
Vậy góc yOz = 70độ .
b, Vì Ot là tia đối của tia Oz , Om là tia đối của tia Ox nên :
góc xOt = góc zOm ( đối đỉnh )
mà góc xOt + góc xOz = 180độ
góc zOm + góc tOm = 180độ
Suy ra : góc xOz = góc tOm
mà góc xOz = 120độ
Vậy góc tOm = 120độ .
c, Vì góc yOm và góc xOy là hai góc kề bù nên :
góc yOm + góc xOy = 180độ
=> góc yOm = 180độ - 50độ
=> góc yOm = 130độ
Vậy góc yOm = 130độ .
Chúc bạn học tốt

Vì tam giác vuông ABC tại điểm A:
Áp dụng định địa lý py-ta-go ta có:
BC^2= AB^2 + AC^2
BC^2 = 3^2 + 4^2
BC^2 = 9+ 16
BC^2 = 25
BC^2 = 5 ( cm )
b) Vì AD = Ab
=> Tam giác ABC cân tại A
c) Xét tam giác AED và tam giác ACB có:
AD = AB ( gt)
A1 = A2 ( 2 góc đối đỉnh )
AE - AC ( gt)
=> Tam giác AED = ACD ( C.g.c )
=> DE + BC ( 2 Cạnh Tương ứng )
a,vì tam giác ABC vuông tại A nên theo định lí Pytago ta có:
AB2+AC2=BC2
\(\Rightarrow\)32+42=BC2
\(\Rightarrow\)25=BC2
\(\Rightarrow\)BC=5 (cm)

Để tạo được một tam giác thì độ dài ba cạnh phải thoả mãn bất đẳng thức tam giác đó là tổng độ dài hai cạnh bất kỳ phải lớn hơn cạnh còn lại.
Vì vậy chỉ có bộ ba độ dài sau thoả mãn (2,3,4); (2,4,5); (3,4,5).
(Lưu ý: để xét cho nhanh, các bạn áp dụng phần Lưu ý (trang 63 sgk Toán 7 Tập 2)), tức là ta so sánh độ dài lớn nhất với tổng hai cạnh hoặc so sánh độ dài nhỏ nhất với hiệu hai cạnh.
Ví dụ với cặp 3 độ dài (1, 2, 3) không là ba cạnh vì:
- bất đẳng thức 3 > 2 + 1 sai
- hoặc bất đẳng thức 3 - 2 < 1 sai)
Trong một tam giác, độ dài một cạnh lớn hơn hiệu và nhỏ hơn tổng của hai cạnh còn lại. Vậy nên với năm đoạn thẳng có độ dài 1cm, 2cm, 3cm, 4cm, 5cm chỉ dựng được tam giác với ba cạnh là các đoạn thẳng có độ dài là các bộ ba 2cm, 3cm, 4cm, bộ ba 3cm, 4cm, 5cm, bộ ba 2cm, 4cm, 5cm.

Gọi 3 cạnh của hình hộp chữ nhật lần lượt là: x; y; z ( cm; >0)
Diện tích 3 mặt lần lượt là: xy ; yz; xz ( cm^2)
( chú ý hình hộp chữ chữ nhật có 4 cạnh bằng x; 4 cạnh =y; 4 cạnh =z )
Theo bài ra ta có: \(\hept{\begin{cases}\frac{xy}{2}=\frac{yz}{3}=\frac{zx}{5}\left(1\right)\\4x+4y+4z=248\left(2\right)\end{cases}}\)
(1) => \(\frac{x}{2}=\frac{z}{3};\frac{y}{3}=\frac{x}{5}\)=> \(\frac{x}{10}=\frac{z}{15}=\frac{y}{6}\)
(2) => \(x+y+z=62\)
Tự làm tiếp nhé!
cm2 với cm3
bạn có thể viết vào bản viết tắt
cm² đo diện tích (kích thước hai chiều, ví dụ như diện tích mặt bàn), còn cm³ đo thể tích (kích thước ba chiều, ví dụ như thể tích nước trong cốc).