Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(\left(a+2b-3c-d\right)\left(a+2b+3c+d\right)\)
\(=\left[\left(a+2b\right)-\left(3c+d\right)\right]\cdot\left[\left(a+2b\right)+\left(3c+d\right)\right]\)
\(=\left(a+2b\right)^2-\left(3c+d\right)^2\)
\(=a^2+4ab+4b^2-9c^2-6cd-d^2\)
( a + 2b - 3c - d )( a + 2b + 3c + d )
= [ ( a + 2b ) - ( 3c + d ) ][ ( a + 2b ) + ( 3c + d ) ]
= ( a + 2b )2 - ( 3c + d )2
= a2 + 4ab + 4b2 - ( 9c2 + 6cd + d2 )
= a2 + 4ab + 4b2 - 9c2 - 6cd - d2

a) ∆ABC có cạnh BC lớn nhất nên chân đường cao kẻ từ A phải nằm giữa B và C
=> HB + HC = BC
∆AHC vuông tại H => HC < AC
∆AHB vuông tại H => HB < AB
Cộng theo vế hai bất đẳng thức ta có:
HB + HC < AC + AB
Hay BC < AC + AB
b) BC là cạnh lớn nhất nên suy ra AB < BC và AC < BC
Do đó AB < BC + AC; AC < BC +AB
(cộng thêm AC hoặc AB vào vế phải của bất đẳng thức)

a) Xét tam giác vuông AHC có AC là cạnh lớn nhất ( cạnh lớn nhất trong tam giác vuông) => AC>HC (1) Xét tam giác vuông AHB có AB là cạnh lớn nhất (canh lớn nhất trong tam giác vuông) =>AB>HB (2) Ta có : HC+HB+BC ( H nằm giũa A và C) (3) Từ (1) , (2) và (3) => AC+AB>BC b)Xét tam giác ABC có BC là cạnh lớn nhất(gt) =>BC>AB Ta có : AC>0 => BC+AC>AB Xét tam giác ABC có BC là cạnh lớn nhất (gt) =>BC>AC Vì AB>0=>BC+AB>AC

a) ∆ABC có cạnh BC lớn nhất nên chân đường cao kẻ từ A phải nằm giữa B và C
=> HB + HC = BC
∆AHC vuông tại H => HC < AC
∆AHB vuông tại H => HB < AB
Cộng theo vế hai bất đẳng thức ta có:
HB + HC < AC + AB
Hay BC < AC + AB
b) BC là cạnh lớn nhất nên suy ra AB < BC và AC < BC
Do đó AB < BC + AC; AC < BC +AB
(cộng thêm AC hoặc AB vào vế phải của bất đẳng thức)

Xét tam giác ABC vì BC là cạnh lớn nhất nên AB < BC và AC < BC.
Mà ta lại có: AC > 0 và AB > 0 hay 0 < AC và 0 < AB
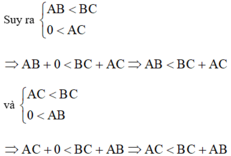
⇒ Đpcm

\(10\cdot9\cdot8\cdot7\cdot6\div\left(5+4\cdot3-2\right)+1=2017\)

Theo giả thiết, tam giác ABC có độ dài cạnh BC là lớn nhất nên chân đường vuông góc kẻ từ A đến cạnh BC chắn chắn phải nằm giữa B và C.
Suy ra H nằm giữa B và C.
⇒ HB + HC = BC
+) Xét tam giác AHB vuông tại H ta có: HB < AB (1) (vì trong tam giác vuông cạnh huyền là cạnh lớn nhất)
+) Xét tam giác AHC vuông tại H ta có: HC < AC (2) (vì trong tam giác vuông cạnh huyền là cạnh lớn nhất)
Lấy (1) + (2) ta được:
HB + HC < AB + AC
Mà HB + HC = BC suy ra BC < AB + AC hay AB + AC > BC