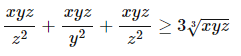Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(BDT\Leftrightarrow a^2+b^2+c^2+2abc+1-2\left(ab+bc+ca\right)\ge0\)
\(\Rightarrow\left(a-b\right)^2+\left(c-1\right)^2+2c\left(a-1\right)\left(b-1\right)\ge0\)
Từ đây ta thấy trong 3 số a,b,c sẽ có 2 số hoặc cùng \(\ge1\) hoặc cùng \(\le1\).giả sử 2 số đó là a và b suy ra \(\left(a-1\right)\left(b-1\right)\ge0\)
Vậy BĐT đầu luôn đúng
Thích Dirichlet thì chơi Dirichlet
Theo nguyên lý Dirichlet thì trong ba số (a - 1); (b - 1); (c - 1) luôn tồn tại ít nhất 2 số cùng dấu.
Không mất tính tổng quát ta giả sử hai số đó là (a - 1) và (b - 1).
\(\Rightarrow\left(a-1\right)\left(b-1\right)\ge0\)
\(\Leftrightarrow2c\left(a-1\right)\left(b-1\right)\ge0\)
\(\Leftrightarrow2abc\ge2\left(ac+bc-c\right)\)
Giờ ta cần chứng minh
\(a^2+b^2+c^2+2\left(ac+bc-c\right)+1\ge2\left(ab+bc+ca\right)\)
\(\Leftrightarrow\left(a-b\right)^2+\left(c-1\right)^2\ge0\)
Dấu = xảy ra khi a = b = c = 1

Cho x,y>0 thỏa mãn x3+y3=x−y. Chứng minh: x2+y2<1.
Cho x,y>0x,y>0 thỏa mãn x3+y3=x−y. Chứng minh: x2+y2<1.
.............................

Bạn tham khảo cách chứng minh tại đây :
Câu hỏi của Nguyễn Huy Thắng - Toán lớp 10 | Học trực tuyến
Áp dụng : Theo BĐT \(AM-GM\) ta có :
\(a+b+c\ge3\sqrt[3]{abc}\)
\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge3\sqrt[3]{\dfrac{1}{abc}}\)
Nhân vế theo vế ta được :
\(\left(a+b+c\right)\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\ge3\sqrt[3]{abc}.3\sqrt[3]{\dfrac{1}{abc}}=3.3.1=9\)
Dấu \("="\) xảy ra khi \(a=b=c\)



I don't now
mik ko biết
sorry
......................
1. \(2ab\le\frac{\left(a+b\right)^2}{2}\le a^2+b^2\) ( \(\forall a;b\))
2. \(\frac{a}{b}+\frac{b}{a}\ge2\)( \(\forall a;b>0\))
3. \(\frac{1}{a}+\frac{1}{b}\ge\frac{4}{a+b}\)\(\left(a;b>0\right)\)
4. \(\frac{1}{ab}\ge\frac{4}{\left(a+b\right)^2}\) \(\left(a;b>0\right)\)
5. \(\left(a^2+b^2\right)\left(c^2+d^2\right)\ge\left(ac+bd\right)^2\)
6. \(a^2+b^2+c^2\ge ab+bc+ca\)
7. \(3\left(a^2+b^2+c^2\right)\ge\left(a+b+c\right)^2\)
8. \(\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\) \(\left(a;b;c>0\right)\)
9. \(\frac{a^2}{x}+\frac{b^2}{y}\ge\frac{\left(a+b\right)^2}{x+y}\)\(\left(x;y>0\right)\)
10. \(\frac{a^2}{x}+\frac{b^2}{y}+\frac{c^2}{z}\ge\frac{\left(a+b+c\right)^2}{x+y+z}\) \(\left(x;y;z>0\right)\)