Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi E là biến cố “Người không thành thạo cả hai thứ tiếng Anh hay Pháp”.
Khi đó \(\overline E \) là biến cố “Người thành thạo tiếng Anh hoặc Pháp”.
Ta có \(\overline E = A \cup B.\)
\( \Rightarrow P\left( E \right) = 1 - P\left( {\overline E } \right) = 1 - P\left( {A \cup B} \right) = 1 - \frac{{47}}{{50}} = \frac{3}{{50}}\)
Vậy xác suất để người được chọn không thành thạo cả hai thứ tiếng Anh hay Pháp là \(\frac{3}{{50}}.\)
Đáp án B.
Sử dụng dữ kiện sau để trả lời các câu hỏi trong các Bài 8.20, 8.21.
Một lớp có 40 học sinh, trong đó có 23 học sinh thích bóng chuyền,18 học sinh thích bóng rổ, 26 học sinh thích bóng chuyền hoặc bóng rổ hoặc cả hai. Chọn ngẫu nhiên một học sinh trong lớp.

a) Gọi A là biến cố “Người mua sách A”; B là biến cố “Người mua sách B”; E là biến cố “Người đó không mua cả sách A và sách B”.
Khi đó \(\overline E \) là biến cố “Người đó mua sách A hoặc sách B”.
Ta có \(\overline E = A \cup B.\)
\(P\left( {\overline E } \right) = P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right) = 50\% + 70\% - 30\% = 90\% \)
Vậy xác suất để người mua đó mua ít nhất một trong hai sách A hoặc B là \(90\% \)
b) Ta có \(P\left( E \right) = 1 - P\left( {\overline E } \right) = 1 - 90\% = 10\% \)
Vậy xác suất để người mua đó không mua cả sách A và sách B là 10%.

Chọn B
Số phần tử của không gian mẫu ![]()
Gọi A là biến cố: “chọn được 4 đại biểu để trong đó mỗi nước đều có 1 đại biểu và có cả đại biểu
nam và đại biểu nữ”
Số cách chọn 4 người đủ các nước tức là có một nước có 2 người, hai nước còn lại, mỗi nước 1 người là:.
![]()
Số cách chọn 4 người đủ các nước và toàn đại biểu nam là:
![]()
Số cách chọn 4 người đủ các nước và toàn đại biểu nữ là:
![]()
Số phần tử của A là n(A) = 2499- 12 - 550 = 1937
Xác suất của biến cố A: ![]()

Đáp án B
Học sinh đó làm đúng được 5 điểm khi làm được đúng 25 câu bất kỳ trong số 50 câu, 25 câu còn lại làm sai.
Xác suất để học sinh là đúng một câu bất kỳ là 1 4 , làm sai một câu là . Do đó xác suất để học sinh đó làm đúng 25 câu bất kỳ trong số 50 câu là C 50 25 . 1 4 25 .
Xác suất để hoạc sinh đó làm sai 25 câu còn lại là 3 4 25 .
Vậy xác suất để học sinh đó làm được đúng 5 điểm là: C 50 25 . 1 4 25 . 3 4 25

Đáp án D
Học sinh đó làm đúng được 5 điểm khi làm được đúng 25 câu bất kỳ trong số 50 câu, 25 câu còn lại làm sai.
Xác suất để học sinh là đúng một câu bất kỳ là 1 4 , làm sai một câu là 3 4 . Do đó xác suất để học sinh đó làm đúng 25 câu bất kỳ trong số 50 câu là C 50 25 . 1 4 25 .
Xác suất để hoạc sinh đó làm sai 25 câu còn lại là 3 4 25 .
Vậy xác suất để học sinh đó làm được đúng 5 điểm là: C 50 25 . 1 4 25 . 3 4 25


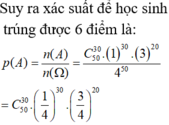
Gọi A là biến cố “Người thành thạo tiếng Anh”; B là biến cố “Người thành thạo tiếng Pháp”.
Khi đó \(P\left( A \right) = \frac{{31}}{{50}},P\left( B \right) = \frac{{21}}{{50}},P\left( {AB} \right) = \frac{5}{{50}} = \frac{1}{{10}}\)
Ta có \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right) = \frac{{31}}{{50}} + \frac{{21}}{{50}} - \frac{1}{{10}} = \frac{{47}}{{50}}\)
Vậy xác suất để người được chọn thành thạo ít nhất một trong hai thứ tiếng Anh hoặc Pháp là \(\frac{{47}}{{50}}.\)
Đáp án A