Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

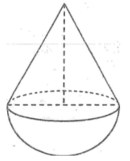
Bán kính đường tròn đáy đồ chơi thứ nhất bằng bán kính nửa hình cầu (3cm)
Vậy chọn đáp án B

*Loại thứ nhất có chiều cao 9cm bao gồm chiều cao của hình nón và bán kính của hình cầu.Mà chiều cao hình nón bằng đường kính hình cầu nên ta có:
2r + r =9 (cm) ⇒ r = 3cm
Chiều cao hình nón là 6cm
Thể tích hình nón:
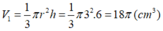
Thể tích nửa hình cầu :
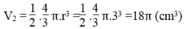
Thể tích loại đồ chơi thứ nhất: V = V 1 + V 2 = 36 π ( c m 3 )
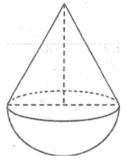
*Loại thứ hai có chiều cao 18cm bao gồm chiều cao của hình nón và bán kính của hình cầu .Mà chiều cao hình nón bằng đường kính hình cầu nên ta có:
2r + r =18 (cm) ⇒ r = 6cm
Chiều cao hình nón là 12cm thể tích hình nón:
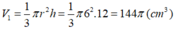
Thể tích nửa hình cầu :
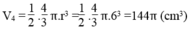
Thể tích loại đồ chơi thứ nhất:
V = V 3 + V 4 = 288 π ( c m 3 )
Vậy t h ể t í c h đ ồ c h ơ i l o ạ i t h ứ h a i t h ể t í c h đ ồ c h ơ i l o ạ i t h ứ n h ấ t = 288 π 36 π =8
Vậy chọn đáp án C

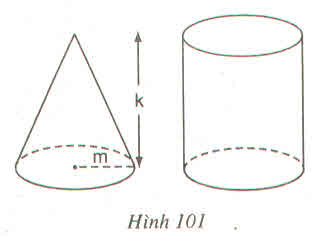
a) Với giả thiết ở đề bài, ta có thể tính được r từ đó tính được diện tích mặt cầu gần bằng \(26cm^2\)
b) Tương tự câu a, ta tính được thể tích hình nón là \(7,9cm^3\)

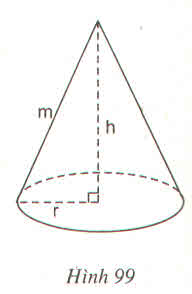
Thể tích hình nón : V = (1/3) π . r 2 h ( c m 3 )
Vậy chọn đáp án B
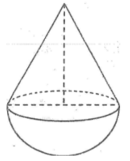


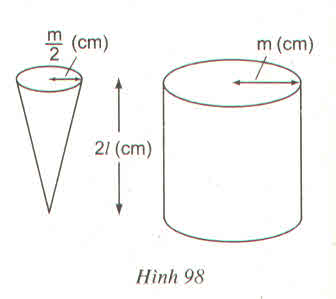

Thể tích đồ chơi loại thứ nhất là 36 π ( c m 3 )
Vậy chọn đáp án B