
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


4:
a: AC=căn 15^2-9^2=12cm
AB<AC<BC
=>góc C<góc B<góc A
b: Xét ΔCBD có
CA vừa là đường cao, vừa là trung tuyến
=>ΔBCD cân tại C
c: Xét ΔCBD có
CA,BE là trung tuyến
CA cắt BE tại I
=>I là trọng tâm
=>DI đi qua trung điểm của BC

4:
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
b: ΔABD=ΔAED
=>\(\widehat{ABD}=\widehat{AED}\)
=>\(\widehat{AED}=90^0\)
=>DE⊥AC
c: AB=AE
DB=DE
Do đó: AD là đường trung trực của BE
=>AD⊥BE
d: Xét ΔAEK vuông tại E và ΔABC vuông tại B có
AE=AB
\(\widehat{EAK}\) chung
Do đó: ΔAEK=ΔABC
=>AK=AC
Xét ΔAKC có AB/AK=AE/AC
nên BE//CK

a)\(-2x^2\) hệ số :-2 biến : x2
b)\(\dfrac{17}{3}xy\) hệ số :17/3 biến xy
c)\(20xy^2\) hệ ssos :20 biến xy2
d)
dạng 2
\(a,-2x+8=0=>-2x=-8=>x=4\)
\(b,-12x+18=0=>-12x=-18=>x=\dfrac{-18}{-12}=\dfrac{3}{2}\)
c)\(2x-1=0=>2x=1=>x=\dfrac{1}{2}\)
d)\(=>\left[{}\begin{matrix}x-3=0\\15+4x=0\end{matrix}\right.=>\left[{}\begin{matrix}x=3\\x=\dfrac{15}{4}\end{matrix}\right.\)
e)\(=>\left[{}\begin{matrix}4x-3=0\\5+x=0\end{matrix}\right.=>\left[{}\begin{matrix}x=\dfrac{3}{4}\\x=-5\end{matrix}\right.\)

`#3107.101107`
`1)`
`75^3 \div (-25)^3`
`= [ 75 \div (-25)]^3`
`= (-3)^3`
`= -27`
`2)`
`(-60)^2 \div (-5)^2`
`= [ (-60) \div (-5)]^2`
`= 12^2`
`= 144`
`3)`
`169^2 \div (-13)^2`
`= 169^2 \div 169`
`= 169`
`4)`
`(1/2)^2 \div (3/2)^2`
`= (1/2 \div 3/2)^2`
`= (1/3)^2`
`= 1/9`
`5)`
`(2/3)^3 \div (8/27)^3`
`= (2/3 \div 8/27)^3`
`= (9/4)^3`
`= 729/64`
`6)`
`(5/4)^4 \div (15/2)^4`
`= (5/4 \div 15/2)^4`
`= (1/6)^4`
`= 1/1296`
`7)`
`(7/8)^5 \div (21/16)^5`
`= (7/8 \div 21/16)^5`
`= (2/3)^5`
`= 32/243`
`8)`
`(5/6)^4 \div (25/18)^4`
`= (5/6 \div 25/18)^4`
`= (3/5)^4`
`= 81/625`
`9)`
`(-3/4)^3 \div (9/8)^3`
`= (-3/4 \div 9/8)^3`
`= (-2/3)^3`
`= -8/27`
`10)`
`(9/10)^6 \div (27/(-20))^6`
`= [ 9/10 \div (-27/20)]^6`
`= (-2/3)^6`
`= 64/729`
`11)`
`(0,2)^10 \div (0,2)^5`
`= (0,2)^5`

Lời giải:
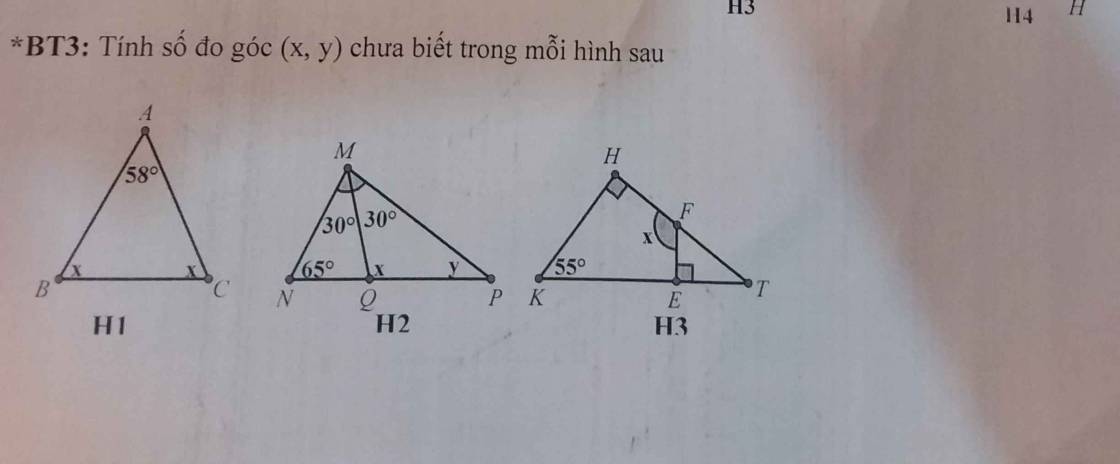
$x+x+58^0=180^0$ (tổng 3 góc trong tam giác)
$\Rightarrow 2x=180^0-58^0=122^0$
$\Rightarrow x=61^0$
--------------------
$x=\widehat{NMQ}+\widehat{MNQ}=30^0+65^0=95^0$
$y=180^0-30^0-x=150^0-95^0=55^0$
--------------------
$x=360^0-55^0-90^0-90^0=125^0$


Bạn cần bài nào ạ? Nếu mà cần tất cả các bài đó thì bạn tách ra từng CH khác nhau để các TV khác giúp đỡ nhé!

a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
b: Xét ΔBDF và ΔEDC có
\(\widehat{BDF}=\widehat{EDC}\)
DB=DE
\(\widehat{DBF}=\widehat{DEC}\)
Do đó: ΔBDF=ΔEDC


 SOS
SOS
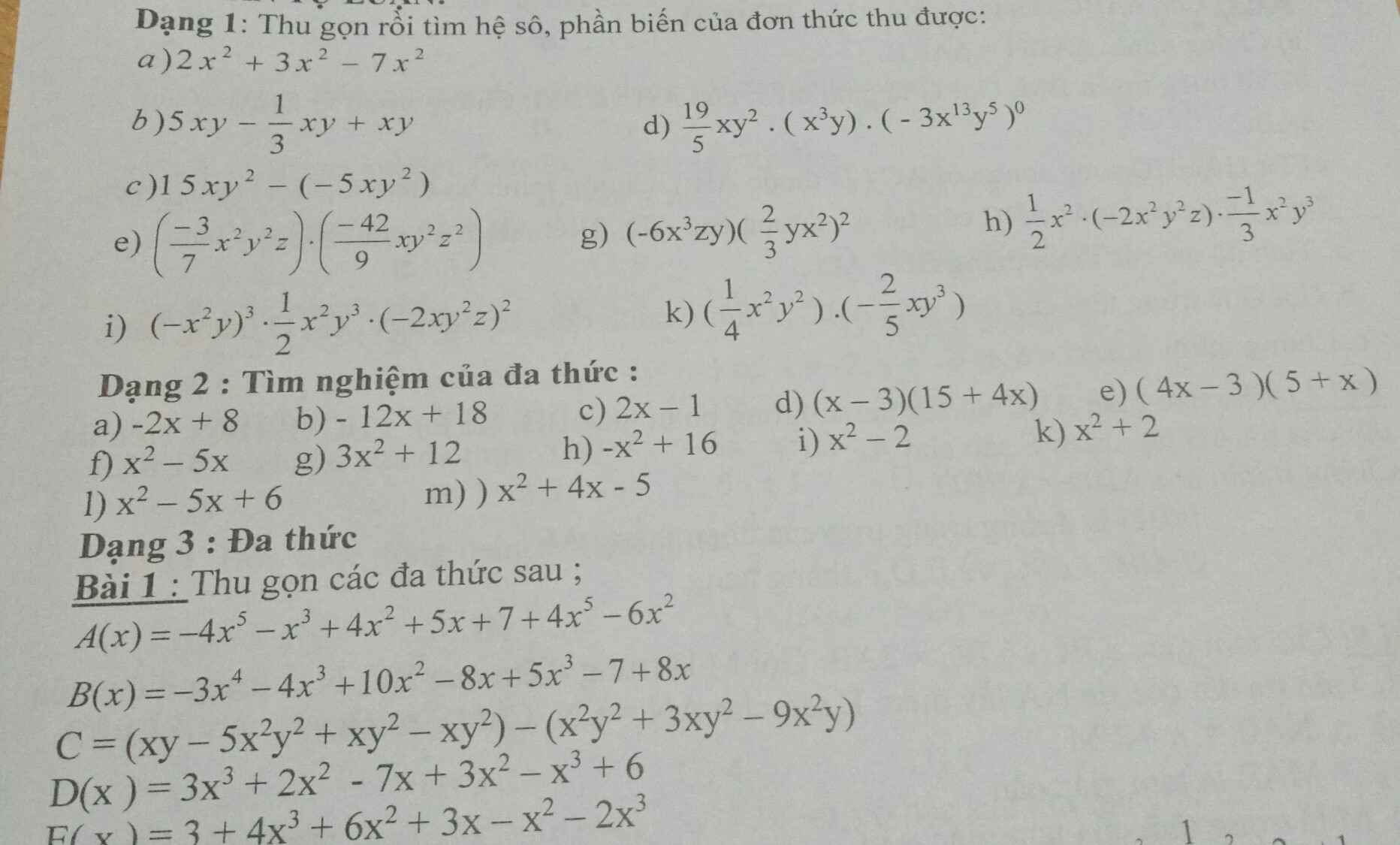






1) \(\dfrac{8^{10}}{4^8}=\dfrac{\left(2^3\right)^{10}}{\left(2^2\right)^8}=\dfrac{2^{30}}{2^{16}}=2^{30-16}=3^{14}\)
2) \(\dfrac{4^2\cdot4^3}{2^{10}}=\dfrac{4^{2+3}}{\left(2^2\right)^5}=\dfrac{4^5}{4^5}=1\)
3) \(\dfrac{8^2\cdot4^5}{2^{20}}=\dfrac{\left(2^3\right)^2\cdot\left(2^2\right)^5}{2^{20}}=\dfrac{2^6\cdot2^{10}}{2^{20}}=\dfrac{2^{16}}{2^{20}}=\dfrac{1}{2^4}=\dfrac{1}{16}\)
4) \(\dfrac{2^7\cdot9^3}{6^5\cdot8^2}=\dfrac{2^7\cdot\left(3^2\right)^3}{2^5\cdot3^5\cdot\left(2^3\right)^2}=\dfrac{2^7\cdot3^6}{2^5\cdot3^5\cdot2^6}=\dfrac{2^7\cdot3}{2^{11}}=\dfrac{3}{2^4}=\dfrac{3}{16}\)
5) \(\dfrac{2^{15}\cdot9^4}{6^6\cdot8^3}=\dfrac{2^{15}\cdot\left(3^2\right)^4}{3^6\cdot2^6\cdot\left(2^3\right)^3}=\dfrac{2^{15}\cdot3^8}{3^6\cdot2^6\cdot2^9}=\dfrac{2^{15}\cdot3^2}{2^{15}}=3^2=9\)
6) \(\dfrac{2^7\cdot9^3}{6^3\cdot8^2}=\dfrac{2^7\cdot\left(3^2\right)^3}{2^3\cdot3^3\cdot\left(2^3\right)^2}=\dfrac{2^7\cdot3^6}{2^3\cdot3^3\cdot2^6}=\dfrac{2^7\cdot3^3}{2^9}=\dfrac{3^3}{2^2}=\dfrac{27}{4}\)