
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Khi x=căn 3/4 thì \(M=\dfrac{1+\dfrac{\sqrt{3}}{2}}{1+\sqrt{1+\dfrac{\sqrt{3}}{2}}}+\dfrac{1-\dfrac{\sqrt{3}}{2}}{1-\sqrt{1-\dfrac{\sqrt{3}}{2}}}\)
\(=\dfrac{\sqrt{2}+\sqrt{6}}{\sqrt{2}+\sqrt{2+\sqrt{3}}}+\dfrac{\sqrt{2}-\sqrt{6}}{\sqrt{2}-\sqrt{2-\sqrt{3}}}\)
\(=\dfrac{2\sqrt{3}+2}{2+\sqrt{3}+1}+\dfrac{2-2\sqrt{3}}{2-\sqrt{3}+1}\)
\(=\dfrac{2\left(\sqrt{3}+1\right)}{\sqrt{3}\left(\sqrt{3}+1\right)}+\dfrac{2\left(1-\sqrt{3}\right)}{\sqrt{3}\left(\sqrt{3}-1\right)}=0\)

4:
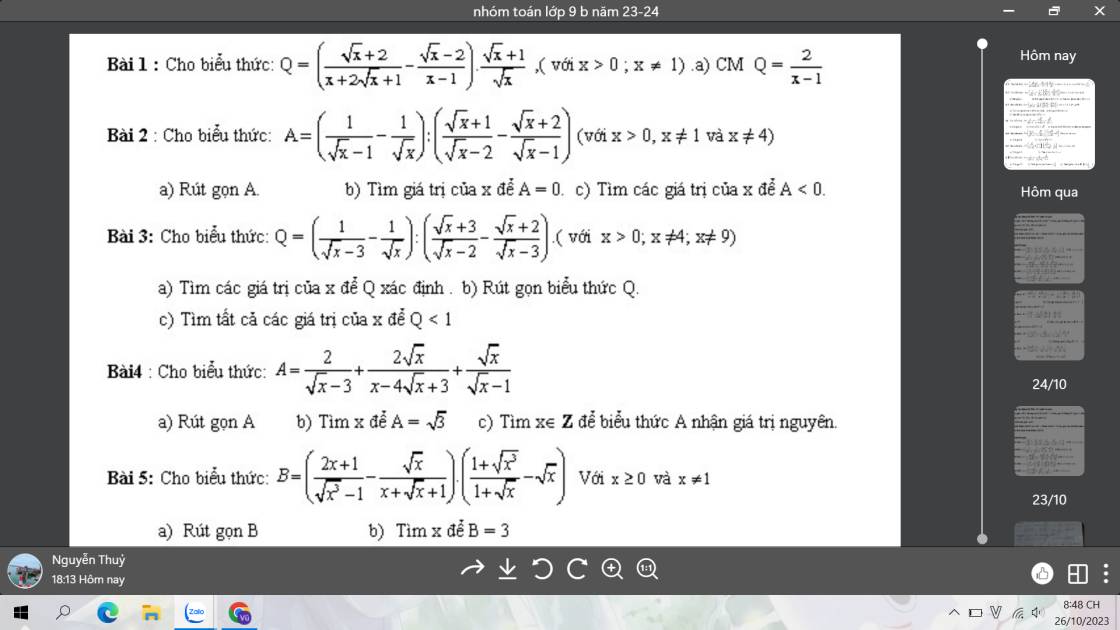
a: ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\notin\left\{1;9\right\}\end{matrix}\right.\)
\(A=\dfrac{2}{\sqrt{x}-3}+\dfrac{2\sqrt{x}}{x-4\sqrt{x}+3}+\dfrac{\sqrt{x}}{\sqrt{x}-1}\)
\(=\dfrac{2}{\sqrt{x}-3}+\dfrac{2\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-3\right)}+\dfrac{\sqrt{x}}{\sqrt{x}-1}\)
\(=\dfrac{2\sqrt{x}-2+2\sqrt{x}+x-3\sqrt{x}}{\left(\sqrt{x}-1\right)\cdot\left(\sqrt{x}-3\right)}\)
\(=\dfrac{x+\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}\)
b: A=căn 3
=>\(\dfrac{\sqrt{x}+2}{\sqrt{x}-3}=\sqrt{3}\)
=>\(\sqrt{x}+2=\sqrt{3}\cdot\sqrt{x}-3\sqrt{3}\)
=>\(\sqrt{x}\left(1-\sqrt{3}\right)=-3\sqrt{3}-2\)
=>\(\sqrt{x}=\dfrac{3\sqrt{3}+2}{\sqrt{3}-1}=\dfrac{11+5\sqrt{3}}{2}\)
=>\(x=\dfrac{98+55\sqrt{3}}{2}\)
c: Để A nguyên thì \(\sqrt{x}-3+5⋮\sqrt{x}-3\)
=>\(\sqrt{x}-3\in\left\{1;-1;5;-5\right\}\)
=>\(\sqrt{x}\in\left\{4;2;8;-2\right\}\)
=>\(\sqrt{x}\in\left\{4;2;8\right\}\)
=>\(x\in\left\{16;4;64\right\}\)

Lời giải:
$2020\equiv 1\pmod 3\Rightarrow 2020x^3\equiv x^3\pmod 3$
$2021\equiv -1\pmod 3\Rightarrow 2021x\equiv -x\pmod 3$
$\Rightarrow 2020x^3+2021x\equiv x^3-x\pmod 3$
Mà $x^3-x=x(x^2-1)=x(x-1)(x+1)$ là tích 3 số nguyên liên tiếp nên $x^3-x\equiv 0\pmod 3$
$\Rightarrow 2020x^3+2021x\equiv 0\pmod 3(*)$
Mặt khác:
$y^{2022}=(y^{1011})^2$ là scp nên $y^{2022}\equiv 0,1\pmod 3$
$2023\equiv 1\pmod 3$
$\Rightarrow y^{2022}+2023\equiv 1,2\pmod 3(**)$
Từ $(*); (**)\Rightarrow 2020x^3+2021x\neq y^{2022}+2023$ với mọi $x,y$ nguyên.
Do đó không tồn tại $x,y$ thỏa đề.
Lời giải:
$2020\equiv 1\pmod 3\Rightarrow 2020x^3\equiv x^3\pmod 3$
$2021\equiv -1\pmod 3\Rightarrow 2021x\equiv -x\pmod 3$
$\Rightarrow 2020x^3+2021x\equiv x^3-x\pmod 3$
Mà $x^3-x=x(x^2-1)=x(x-1)(x+1)$ là tích 3 số nguyên liên tiếp nên $x^3-x\equiv 0\pmod 3$
$\Rightarrow 2020x^3+2021x\equiv 0\pmod 3(*)$
Mặt khác:
$y^{2022}=(y^{1011})^2$ là scp nên $y^{2022}\equiv 0,1\pmod 3$
$2023\equiv 1\pmod 3$
$\Rightarrow y^{2022}+2023\equiv 1,2\pmod 3(**)$
Từ $(*); (**)\Rightarrow 2020x^3+2021x\neq y^{2022}+2023$ với mọi $x,y$ nguyên.
Do đó không tồn tại $x,y$ thỏa đề.

\(\sin^2\alpha+\cos^2\alpha=1\)
\(\Rightarrow\cos\alpha=\sqrt{1-\sin^2\alpha}=\sqrt{1-\frac{1}{4}}=\frac{\sqrt{3}}{2}\)
\(\Rightarrow\tan\alpha=\frac{\sin\alpha}{\cos\alpha}=\frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}}=\frac{1}{\sqrt{3}}\)


a: Thay x=0 và y=5 vào (d), ta được:
m*0+5=5
=>5=5(đúng)
=>ĐPCM
b: x1<x2; |x1|>|x2|
=>x1*x2<0
PTHĐGĐ là:
x^2-mx-5=0
Vì a*c<0
nên x1,x2 luôn trái dấu
=>Với mọi m
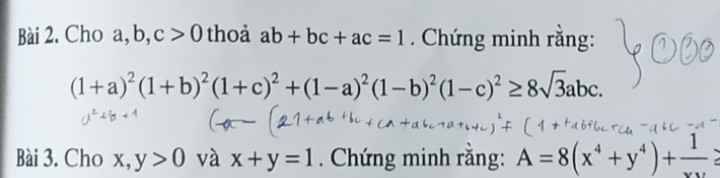
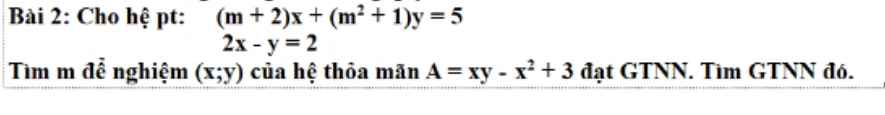
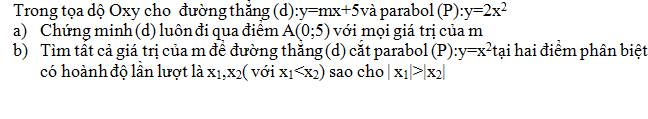
Người ra đề cho con số tào lao quá, dẫn tới đẳng thức của BĐT này ko xảy ra. (vế trái lớn hơn vế phải tuyệt đối, thậm chí là hơn rất xa).
Ta có:
\(ab+bc+ca\ge3\sqrt[3]{a^2b^2c^2}\Rightarrow abc\le\dfrac{1}{3\sqrt{3}}\)
\(\Rightarrow8\sqrt{3}abc\le\dfrac{8}{3}\)
Đặt vế trái BĐT cần chứng minh là P:
\(P=\left[\left(a+1\right)\left(b+1\right)\left(c+1\right)\right]^2+\left[\left(a-1\right)\left(b-1\right)\left(c-1\right)\right]^2\)
\(=\left(abc+a+b+c+ab+bc+ca+1\right)^2+\left(abc+a+b+c-ab-bc-ca-1\right)^2\)
\(=\left(abc+a+b+c+2\right)^2+\left(abc+a+b+c-2\right)^2\)
\(=\left(abc+a+b+c\right)^2+4>\dfrac{8}{3}\ge8\sqrt{3}abc\) (đpcm)