
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 11:
Ta có \(n^2+5n+9\) là bội của \(n+1\) khi:
\(\dfrac{n^2+5n+9}{n+3}\) có giá trị nguyên:
\(=\dfrac{n^2+3n+2n+9}{n+3}=\dfrac{n\left(n+3\right)+2n+9}{n+3}\)
\(=n+\dfrac{2n+9}{n+3}=n+\dfrac{2n+6+3}{n+3}=n+2+\dfrac{3}{n+3}\)
⇒ \(\dfrac{3}{n+3}\) phải có giá trị nguyên:
\(\Rightarrow3\) ⋮ n + 3
⇒ n + 3 ∈ Ư(3)
⇒ n + 3 ∈ {1; -1; 3; -3}
⇒ n ∈ {-2; -4; 0; -6}
Vậy: ...



a) x + 10 = 20
x = 20 - 10
x = 10
b) 2x + 15 = 35
2x = 35 - 15
2x = 20
x = 20 : 2
x = 10
c) 3(x + 2) = 15
x + 2 = 15 : 3
x + 2 = 5
x = 5 - 2
x = 3
d) 10x + 15.11 = 20.11
10x = 20.11 - 15.11
10x = (20 - 15).11
10x = 5.11
10x = 55
x = 55 : 10
x = 5,5 (không là số tự nhiên)
Vậy không tìm được x thỏa mãn đề bài
e) 4(x + 2) = 3.4
4(x + 2) = 12
x + 2 = 12 : 4
x + 2 = 3
x = 3 - 2
x = 1
f) 33x + 135 = 26.9
33x + 135 = 234
33x = 234 - 135
33x = 99
x = 99 : 33
x = 3
g) 2x + 15 + 16 + 17 = 100
2x + 48 = 100
2x = 100 - 48
2x = 52
x = 52 : 2
x = 26
h) 2(x + 9 + 10 + 11) = 4.12.25
2(x + 30) = 1200
x + 30 = 1200 : 2
x + 30 = 600
x = 600 - 30
x = 570

ngày 1 : 40 trang , ngày 2 : 60 trang , ngày 3 : 20 trang

Bài 117: Tìm số tự nhiên \(x\) biết rằng:
a, 270 \(⋮\) \(x\), 690 \(⋮\) \(x\) và 5 < \(x\) < 30
270 = 2.33.5; 690 = 2.3.5.23
ƯCLN(270; 690) = 2.3.5 = 30
270⋮\(x\); 690 \(⋮\) \(x\) ⇒ \(x\) \(\in\) ƯC(270; 690)
⇒ \(x\) \(\in\){ 1; 2; 3; 5; 6; 10; 15; 30}
Vì 5 < \(x\) < 30 nên \(x\) \(\in\) { 6; 10; 15}
117b, \(x\)max và 120 ⋮ \(x\); 105 ⋮ \(x\)
⇒ \(x\) là ước chung lớn nhất của 120 và 105
120 = 23.3.5; 105 = 3.5.7
ƯCLN (120; 105) = 3.5 = 15 ⇒ \(x\) = 15

Lời giải:
$A> \frac{1}{150}+\frac{1}{150}+....+\frac{1}{150}=\frac{50}{150}=\frac{1}{3}$
$A< \frac{1}{100}+\frac{1}{100}+....+\frac{1}{100}=\frac{50}{100}=\frac{1}{2}$
Vậy $\frac{1}{3}< A< \frac{1}{2}$
Ta có điều phải chứng minh.

 sos giúp tớ với sos
sos giúp tớ với sos


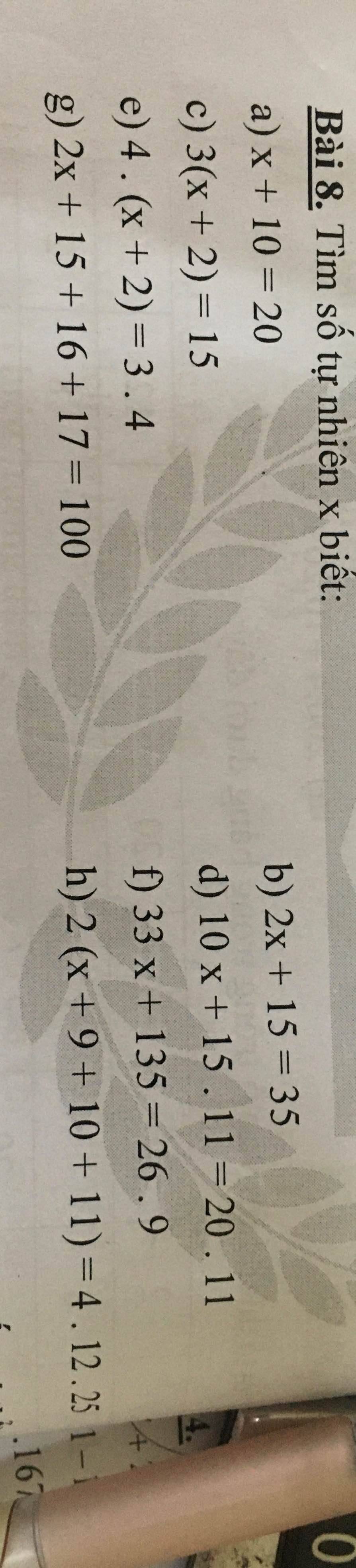

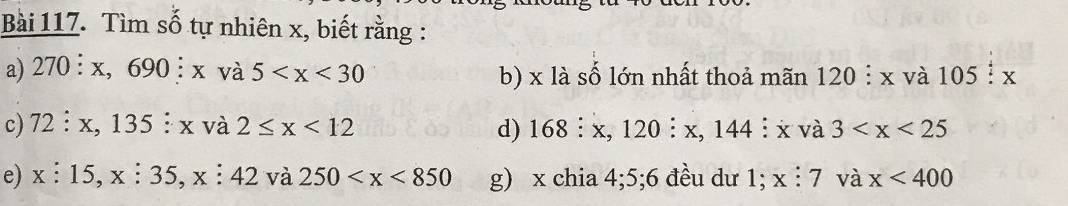

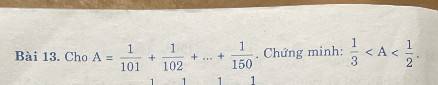 SOS
SOS