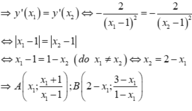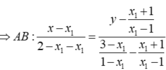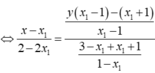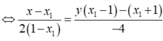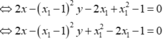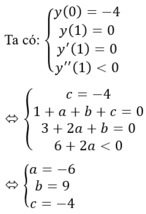Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Phương pháp:
Cho hàm số y = f(x) và M( x 0 ; y 0 )
Bước 1: Gọi ( ∆ ) là tiếp tuyến của đồ thị hàm số đã cho của đồ thị hàm số y = f(x); ( ∆ ) đi qua M( x 0 ; y 0 ) và có hệ số góc k.
Bước 2: (
∆
) có dạng 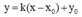
Để (
∆
) tiếp xúc với đồ thị y = f(x) thì hệ 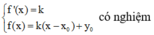
Bước 3: Giải hệ bằng phương pháp thế, số nghiệm của hệ là số tiếp tuyến ( ∆ ) tìm được.
Cách giải:
Gọi k là hệ số góc tiếp tuyến ( ∆ ) với đồ thị (C) đi qua A(1;-6)
=>( ∆ ) có dạng: y = k(x-1) - 6
Để (
∆
) tiếp xúc với (C) thì 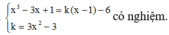
![]()
![]()
![]()
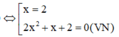
Vậy có 1 pttt đi qua A(1;-6).

y' = 3 - 12x
Đường thẳng (d) có hệ số góc là k đi qua M(1;3) y=k(x-1)+3 .
Đường thẳng (d) tiếp xúc với đồ thì hàm số khi hệ phương trình sau có nghiệm
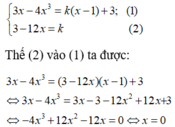
Với x = 0 thì k = 3
Do đó có tối đa hai tiếp tuyến đi qua điểm M(1;3).
Chọn B

Ta có : \(y'=3x^2-2\left(m-1\right)x+3m+1\)
Gọi \(M\left(x_0;y_0\right)\) là tiếp điểm, ta có : \(x_0=1\Rightarrow y_0=3m+1,y'\left(1\right)=m+6\)
Phương trình tiếp tuyến tại M : \(y=\left(m+6\right)\left(x-1\right)+3m+1\)
Tiếp tuyến đi qua A \(\Leftrightarrow-1=m+6+3m+1\Leftrightarrow m=-2\)
Vậy m = -2 là giá trị cần tìm

Chọn: D
Giả sử tiếp điểm là M x 0 ; y 0
Phương trình tiếp tuyến d của đồ thị hàm số y = x3 - 3x2 + 2 tại M x 0 ; y 0 là
![]()
![]()
Do d đi qua điểm A(3; 2) nên
![]()
![]()
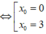
Vậy, có 2 tiếp tuyến của đồ htij hàm số y = x3 - 3x2 + 2 đi qua điểm A(3; 2)

a)
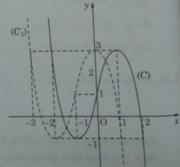
b) Tịnh tiến (C) song song với trục Ox sang trái 1 đơn vị, ta được đồ thị (C1) của hàm số.
y = f(x) = − ( x + 1 ) 3 + 3(x + 1) + 1 hay f(x) = − ( x + 1 ) 3 + 3x + 4 (C1)
Lấy đối xứng (C1) qua trục Ox, ta được đồ thị (C’) của hàm số y = g(x) = ( x + 1 ) 3 − 3x – 4
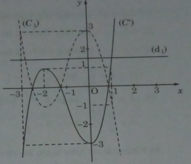
c) Ta có: ( x + 1 ) 3 = 3x + m (1)
⇔ ( x + 1 ) 3 − 3x – 4 = m – 4
Số nghiệm của phương trình (1) là số giao điểm của hai đường :
y = g(x) = ( x + 1 ) 3 − 3x – 4 (C’) và y = m – 4 (d1)
Từ đồ thị, ta suy ra:
+) m > 5 hoặc m < 1: phương trình (1) có một nghiệm.
+) m = 5 hoặc m = 1 : phương trình (1) có hai nghiệm.
+) 1 < m < 5 , phương trình (1) có ba nghiệm.
d) Vì (d) vuông góc với đường thẳng:
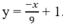
nên ta có hệ số góc bằng 9.
Ta có: g′(x) = 3 ( x + 1 ) 2 – 3
g′(x) = 9 ⇔ 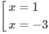
Có hai tiếp tuyến phải tìm là:
y – 1 = 9(x – 1) ⇔ y = 9x – 8;
y + 3 = 9(x + 3) ⇔ y = 9x + 24.

Phương trình tiếp tuyến tại điểm ![]() là
là 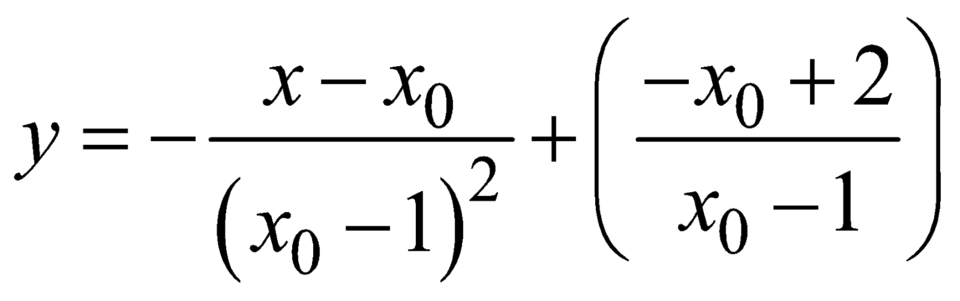
Tiếp tuyến đi qua điểm A suy ra 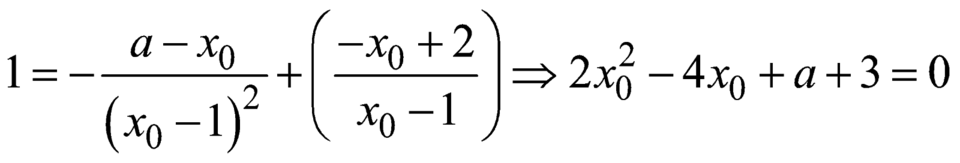 có duy nhất nghiệm khi a=1. Số phần tử của S là 1.
có duy nhất nghiệm khi a=1. Số phần tử của S là 1.
Đáp án B

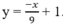
 ]
]