Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bạn ơi câu đàu tiên phải là "của tứ giác ABCD" nhé, mình đánh máy nhầm.
Mà bạn là VIP bias T.O.P đúng hơm,y chang mình. Kết bạn nhoa~
Gọi O là giao điểm 2 đường chéo AC và BD cảu tứ giác ABCD.
Xét tam giác AOB, theo bất đẳng thúc tam giác, ta có: AB<OA+OB
Xét tam giác COD, theo bất đẳng thức tam giác, ta có: CD<OC+OD
Suy ra: AB+CD<OA+OB+OC+OD
hay AB+CD<AC+BD (1)
Ta lại có: AB+BD+AD=<AC+CD+AD
\(\Rightarrow\) AB+BD=<AC+CD
\(\Rightarrow\) AB-CD=<AC-BD (2)
Từ (1) và (2), suy ra: 2AB<2AC (cộng vế theo vế)
\(\Rightarrow\) AB<AC (đpcm)
Đảm bảo chính xác 100%
Độ tin cậy không cần bàn cãi.
Hình như mình đã nhắc nhở bạn một lần về việc không đăng quá nhiều lần 1 bài toán nhưng bạn vẫn làm vậy. Lần sau mình xin phép sẽ xóa hết nhé!
Lời giải:
$3\widehat{A}+2\widehat{B}=180^0$
$\Rightarrow \widehat{A}+\widehat{B}< 90^0\Rightarrow \widehat{C}>90^0$
Do đó trong tam giác $ABC$ thì $AB$ là cạnh lớn nhất. Trên $AB$ lấy $M$ sao cho $AM=AC$
Ta có:
$\widehat{AMC}=\frac{180^0-\widehat{A}}{2}$
$\Rightarrow \widehat{BMC}=180^0-\frac{180^0-\widehat{A}}{2}=180^0-\frac{3\widehat{A}+2\widehat{B}-\widehat{A}}{2}$
$=180^0-(\widehat{A}+\widehat{B})=\widehat{ACB}$
Do đó:
$\triangle ACB\sim \triangle CMB$ (g.g)
$\Rightarrow \frac{AB}{CB}=\frac{CB}{MB}$
$\Rightarrow AB.MB=BC^2$
$\Leftrightarrow AB(AB-AM)=BC^2$
$\Leftrightarrow AB^2-AB.AC=BC^2$.
Nếu $(AB,BC,AC)=(k, k+2, k+4)$ thì:
$k^2-k(k+4)=(k+2)^2$
$\Leftrightarrow k^2+8k+4=0$
$\Leftrightarrow k=-4\pm 2\sqrt{3}$ (loại vì $k$ tự nhiên)
Nếu $(AB, BC, AC)=(k+2, k, k+4)$ thì:
$(k+2)^2-(k+2)(k+4)=k^2$
$\Leftrightarrow k^2+2k+4=0$
$\Leftrightarrow (k+1)^2=-3< 0$ (vô lý)
Vậy không tìm được chu vi.
Bài 8: Vì em nhắn tin nhờ cô giảng bài 8 nên cô chỉ giảng bài 8 thôi nhé
Gọi các cạnh góc vuông, cạnh huyền của tam giác cần tìm lần lượt là: a; b; c
Theo bài ra ta có: a+b+c =36; \(\dfrac{a}{b}\) = \(\dfrac{3}{4}\)
\(\dfrac{a}{b}\) = \(\dfrac{3}{4}\) ⇒ \(\dfrac{a}{3}\) = \(\dfrac{b}{4}\) ⇒ \(\dfrac{a^2}{9}\) = \(\dfrac{b^2}{16}\) = \(\dfrac{a^2+b^2}{9+16}\) (1)
Vì tam giác vuông nên ta theo pytago ta có: a2 + b2 = c2 (2)
Thay (2) vào (1) ta có: \(\dfrac{a^2}{9}\) = \(\dfrac{b^2}{16}\) = \(\dfrac{c^2}{25}\)
⇒ \(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}\) = \(\dfrac{a+b+c}{3+4+5}\) = \(\dfrac{36}{12}\) = 3
a = 3.3 = 9 (cm)
b = 3.4 = 12 (cm)
c = 3.5 = 15 (cm)
Kết luận: độ dài cạnh bé của góc vuông là: 9 cm
dộ dài cạnh lớn của góc vuông là 12 cm
độ dài cạnh huyền là 15 cm
Bài 9:
a,Gọi độ dài cạnh góc vuông là: a
Theo pytago ta có: a2 + a2 = 22 = 4 ⇒ 2a2 = 4 ⇒ a2 = 2 ⇒ a = \(\sqrt{2}\)
b, Gọi độ dài cạnh góc vuông là :b
Theo pytago ta có:
b2 + b2 = 102 =100 ⇒ 2b2 = 100 ⇒ b2 = 50⇒ b = 5\(\sqrt{2}\)
Bài 8 cô làm rồi nhé.
Bài 10 ; Gọi độ dài các cạnh góc của tam giác vuông lần lượt là:
a; b theo bài ra ta có:
\(\dfrac{a}{5}\) = \(\dfrac{b}{12}\) \(\Rightarrow\) \(\dfrac{a^2}{25}\) = \(\dfrac{b^2}{144}\) = \(\dfrac{a^2+b^2}{25+144}\) (1)
Theo pytago ta có: a2 + b2 = 522 = 2704 (2)
Thay (2) vào (1) ta có: \(\dfrac{a^2}{25}\) = \(\dfrac{b^2}{144}\) = \(\dfrac{2704}{169}\) = 16
⇒ a2 = 25.16 = (4.5)2 ⇒ a = 20
b2 = 144.16 = (12.4)2 ⇒ b = 48
Chu vi tam giác ABC là: AB + BC + CA = 3 + 7 + 5 = 15 (cm)
Δ A’B’C’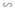 
ΔABC ⇒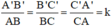 
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
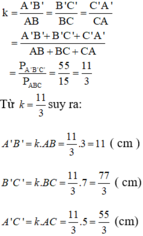
Gọi \(x;x+1;x+2\) lần lượt là các cạnh của ta giác \(\left(x\inℤ^+\right)\)
Theo đề bài ta có :
\(x+x+1+x+2\le100\)
\(\Rightarrow3x+3\le100\)
\(\Rightarrow x\le\dfrac{97}{3}\)
\(\Rightarrow x\in\left\{1;2;...32\right\}\) \(\left(x\inℤ^+\right)\)
Nên sẽ có 33 tam giác thỏa mãn đề bài.
Để có tam giác vuông khi :
\(x^2+\left(x+1\right)^2=\left(x+2\right)^2\left(Pitago\right)\)
\(\Rightarrow x^2+x^2+2x+1=x^2+4x+4\)
\(\Rightarrow x^2-2x-3=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-1\left(loại\right)\\x=3\left(nhận\right)\end{matrix}\right.\) \(\left(a-b+c=0\right)\)
Vậy có 1 tam giác vuông có các cạnh lần lượt là \(3;4;5\)
x\(\ne\)1(vì 1+2=3)