TP
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
N
2
27 tháng 7 2018
\(a,2^{700}=\left(2^7\right)^{100}=128^{100}\)
\(5^{300}=\left(5^3\right)^{100}=125^{100}\)
Có \(128^{100}>125^{100}\Rightarrow2^{700}>5^{300}\)
\(b,S=1+2+2^2+...+2^{50}\)
\(\Rightarrow2S=2+2^2+2^3+...+2^{51}\)
\(\Rightarrow2S-S=S=2^{51}-1< 2^{51}\)
27 tháng 7 2018
a) Ta có :
\(2^{700}=\left(2^7\right)^{100}=128^{100}\)
\(5^{300}=\left(5^3\right)^{100}=125^{100}\)
Vì \(128^{100}>125^{100}\)\(\Rightarrow\)\(2^{700}>5^{300}\)
Vậy \(2^{700}>5^{300}\)
b) \(S=1+2+2^2+...+2^{50}\)
\(\Rightarrow2S=2+2^2+2^3+...+2^{51}\)
\(\Rightarrow2S-S=\left(2+2^2+2^3+...+2^{51}\right)-\left(1+2+2^2+...+2^{50}\right)\)
\(\Rightarrow S=2^{51}-1< 2^{51}\)
Vậy S < 251
_Chúc bạn học tốt_
MT
16 tháng 1 2016
Ta có: 3500=(35)100=243100
2700=(27)100=128100
Vì 243>128 nên: 243100>128100
hay 3500>2700
M
5
10 tháng 8 2017
Ta có : 2700 = (27)100 = 128100
5300 = (53)100 = 125100
Vì : 128100 > 125100
Nên : 2700 > 5300
TH
0
25 tháng 9 2017
a) \(2^{300}=\left(2^3\right)^{100}=8^{100}\)
\(3^{200}=\left(3^2\right)^{100}=9^{100}\)
vi \(8^{100}< 9^{100}\)nen \(2^{300}< 3^{200}\)
ND
19 tháng 4 2020
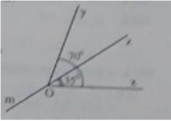
a) tia nằm giữa hai tia còn lại là : tia Ox
b) yOx lớn hơn xOy
c) có
ý c mik ko biết có đúng ko hii
DN
11 tháng 8 2015
1)Ta có:
\(111...11222...22\left(100 cs 1 v\text{à} 2\right)=10^{100}.111...111\left(100 cs 1\right)+222...22\left(100 cs 2\right)\)
\(=10^{100}.\frac{10^{100}-1}{9}+2.\frac{10^{100}-1}{9}=\frac{10^{100}\left(10^{100}-1\right)+2\left(10^{100}-1\right)}{9}=\frac{\left(10^{100}+2\right)\left(10^{100}-1\right)}{9}=\frac{10^{100}+2}{3}.\frac{10^{100}-1}{3}\)
\(M\text{à} \frac{10^{100}+2}{3}\ne\frac{10^{100}-1}{3} \)
\(\Rightarrow111...11222..2\left(100 cs 1 v\text{à} 2\right) \) không phải là tích 2 số tự nhiên
2) Để dacb chia hết cho 4 thì cb chia hết cho 4
Ta có :
cb=10c+b=8c+2c+b
Mà 8c chia hết cho 4 nên
2c+b cũng phải chia hết cho 4(đpcm)
PM
3
điền dấu > nha
k mik
đúng
Ta có :
a6b + 5c0 + d141
= 100a + 60 + b + 500 + 10c + 1000d + 141
= ( 1000d + 100a + 10c + b ) + ( 60 + 500 + 141 )
= dacb + 701 > dacb + 700