PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
16 tháng 1 2019
1. \(a< b\Leftrightarrow2a< 2b\Leftrightarrow2a+1< 2b+1\)
\(a< b\Leftrightarrow-3a>-3b\Leftrightarrow-3a>-3b-1\)
2.\(a>b>0\Leftrightarrow a.\frac{1}{ab}>b.\frac{1}{ab}\Leftrightarrow\frac{1}{b}>\frac{1}{a}\Leftrightarrow\frac{1}{a}< \frac{1}{b}\)
XO
20 tháng 6 2021
Ta có A = 2018.2020 + 2019.2021
= (2020 - 2).2020 + 2019.(2019 + 2)
= 20202 - 2.2020 + 20192 + 2.2019
= 20202 + 20192 - 2(2020 - 2019) = 20202 + 20192 - 2 = B
=> A = B
b) Ta có B = 964 - 1= (932)2 - 12
= (932 + 1)(932 - 1) = (932 + 1)(916 + 1)(916 - 1) = (932 + 1)(916 + 1)(98 + 1)(98 - 1)
= (932 + 1)(916 + 1)(98 + 1)(94 + 1)(94 - 1)
= (932 + 1)(916 + 1)(98 + 1)(94 + 1)(92 + 1)(92 - 1)
(932 + 1)(916 + 1)(98 + 1)(94 + 1)(92 + 1).80
mà A = (932 + 1)(916 + 1)(98 + 1)(94 + 1)(92 + 1).10
=> A < B
XO
20 tháng 6 2021
c) Ta có A = \(\frac{x-y}{x+y}=\frac{\left(x-y\right)\left(x+y\right)}{\left(x+y\right)^2}=\frac{x^2-y^2}{x^2+2xy+y^2}< \frac{x^2-y^2}{x^2+xy+y^2}=B\)
=> A < B
d) \(A=\frac{\left(x+y\right)^3}{x^2-y^2}=\frac{\left(x+y\right)^3}{\left(x+y\right)\left(x-y\right)}=\frac{\left(x+y\right)^2}{x-y}=\frac{x^2+2xy+y^2}{x-y}< \frac{x^2-xy+y^2}{x-y}=B\)
=> A < B
KY
28 tháng 11 2019
1)Ta co
n5-5n3+4n
=n(n4-5n2+4)
=n(n4-n2-4n2+4)
=n(n2(n2-1)-4(n2-1)
=n(n2-4)(n2-1)
=n(n-1)(n+1)(n+2)(n-2)
vi n(n-1)(n+1)(n-2)(n+2) la h 5 so tu nhien lien tiep nen chia het cho 3,5,8 ma 3.5.8=120
=>n5-5n3+4n chia het 120
21 tháng 4 2018
Ta có: \(a>b>0\)
\(\Rightarrow a^2>b^2\)
\(\Rightarrow a^2+a>b^2+b\)
\(\Rightarrow a^2+a+1>b^2+b+1\)
\(\Rightarrow\frac{1}{a^2+a+1}< \frac{1}{b^2+b+1}\)
\(\Rightarrow x< y\)
1 tháng 11 2018
\(x=\frac{a+1}{a^2+a+1}=1-\frac{a^2}{a+a+1}\)
\(y=\frac{b+1}{1+b+b^2}=1-\frac{b^2}{1+b+b^2}\)
Do \(\frac{a^2}{a^2+a+1}>\frac{b^2}{b^2+b+1}\Rightarrow x< y\)
5 tháng 5 2017
a. Do \(a>0,\) \(b>0\) \(\Rightarrow a,b\) là số dương
Ta có:
* \(a< b\Leftrightarrow a^2< ab\) (nhân cả hai vế với a)
* \(a< b\Leftrightarrow ab< b^2\) (nhân cả hai vế với b)
b. Từ câu a theo tính chất bắc cầu suy ra:\(a^2< b^2\)
Ta có: \(a^2< b^2\Leftrightarrow a^3< ab^2\) (nhân cả hai vế với a)
mà ab2<b3 (a<b)
\(\Rightarrow a^3< b^3\)
VK
22 tháng 4 2017
a) Từ a + 5 < b + 5
=> a + 5 + (-5) < b + 5 + (-5) (cộng hai vế với -5)
=> a < b
8 tháng 4 2021
a)từ a+5<b+5 ta cộng -5 vào 2 vế được a<b
b)từ -3a>-3b ta nhân 2 vế với -1/3 (tức là chia cả 2 vế cho -3) và -3a . -1/3< -3b . -1/3 sẽ được a<b
22 tháng 7 2016
a) Ta có : \(\left(x-1\right)^2\ge0\Leftrightarrow x^2-2x+1\ge0\Leftrightarrow x^2+1\ge2x\Leftrightarrow\frac{x^2+1}{x}\ge2\Leftrightarrow x+\frac{1}{x}\ge2\)(vì x > 0)
b) \(\left(x+1\right)^2\ge0\Leftrightarrow x^2+2x+1\ge0\Leftrightarrow x^2+1\ge-2x\Leftrightarrow\frac{x^2+1}{x}\le-2\Leftrightarrow x+\frac{1}{x}\le-2\)(vì x < 0)
22 tháng 7 2016
a) Ta có: \(x+\frac{1}{x}-2=\frac{x^2-2x+1}{x}=\frac{\left(x-1\right)^2}{x}\)
Vì \(x>0,\left(x-1\right)^2\ge0\)nên \(x++\frac{1}{x}-2\ge0\)
Vậy \(x+\frac{1}{x}\ge2\)vs \(x>0\)
b) Ta có: \(x+\frac{1}{x}+2=\frac{x^2+2x+1}{x}=\frac{\left(x+1\right)^2}{x}\)
Vì \(x< 0,\left(x+1\right)^2\le0\), nên \(x+\frac{1}{x}\le0\)
Vậy \(x+\frac{1}{x}\le-2\)vs \(x< 0\)
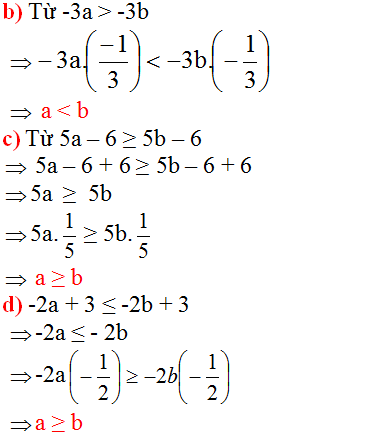
Ta có: x > 2 ⇔ (a – b)x < 2(a – b)
⇒ a – b < 0 ⇔ a < b