Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a ) \(2\sqrt{45}+\sqrt{5}-3\sqrt{80}\)
= \(2\sqrt{9.5}+\sqrt{5}-3\sqrt{16.5}\) \
= \(2.3\sqrt{5}+\sqrt{5}-3.4\sqrt{5}\)
= \(6\sqrt{5}+\sqrt{5}-12\sqrt{5}\)
= \(\left(6+1-12\right)\sqrt{5}\)
= \(-5\sqrt{5}\)
b ) \(\sqrt{\left(2-\sqrt{3}\right)^2}+\dfrac{2}{\sqrt{3}+1}-6\sqrt{\dfrac{16}{3}}\)
= / \(2-\sqrt{3}\) / \(+\dfrac{2.\left(\sqrt{3}-1\right)}{\left(\sqrt{3}+1\right).\left(\sqrt{3}-1\right)}-6\sqrt{\dfrac{48}{3^2}}\)
= \(2-\sqrt{3}+\dfrac{2.\left(\sqrt{3}-1\right)}{\sqrt{3}^2-1^2}-\dfrac{6}{3}\sqrt{48}\)
= \(2-\sqrt{3}+\dfrac{2.\left(\sqrt{3}-1\right)}{3-1}-2\sqrt{48}\)
=\(2-\sqrt{3}+\sqrt{3}-1-2\sqrt{16.3}\)
= \(2-\sqrt{3}+\sqrt{3}-1-8\sqrt{3}\)
= \(1-8\sqrt{3}\)
ý c ) em không biết làm ☹
Trình tự dựng gồm 3 bước:
- Dựng đoạn thẳng BC = 6cm
- Dựng cung chứa góc 40o trên đoạn thẳng BC.
- Dựng đường thẳng xy song song với BC và cách BC một khoảng là 4cm như sau:
Trên đường trung trực d của đoạn thẳng BC lấy đoạn HH' = 4cm (dùng thước có chia khoảng mm). Dựng đường thẳng xy vuông góc với HH' tại H
Gọi giao điểm xy và cung chứa góc là ,
. Khi đó tam giác ABC hoặc A'BC đều thỏa yêu cầu của đề toán
Cách dựng:
+ Dựng đoạn thẳng BC = 6cm.
+ Dựng cung chứa góc 40º trên đoạn thẳng BC (tương tự bài 46) :
Dựng tia Bx sao cho 
Dựng tia By ⊥ Bx.
Dựng đường trung trực của BC cắt By tại O.
Dựng đường tròn (O; OB).
Cung lớn BC chính là cung chứa góc 40º dựng trên đoạn BC.
+ Dựng đường thẳng d song song với BC và cách BC một đoạn 4cm:
Lấy D là trung điểm BC.
Trên đường trung trực của BC lấy D’ sao cho DD’ = 4cm.
Dựng đường thẳng d đi qua D’ và vuông góc với DD’.
+ Đường thẳng d cắt cung lớn BC tại A.
Ta được ΔABC cần dựng.
Chứng minh:
+ Theo cách dựng có BC = 6cm.
+ A ∈ cung chứa góc 40º dựng trên đoạn BC
+ A ∈ d song song với BC và cách BC 4cm
⇒ AH = DD’ = 4cm.
Vậy ΔABC thỏa mãn yêu cầu đề bài.
Biện luận: Do d cắt cung lớn BC tại hai điểm nên bài toán có hai nghiệm hình.
Trên BC lấy I sao cho IC=IB
Ta có AM=MC=AC/2=20/2= 10 cm
Từ M kẻ MH vuông góc AB. Theo gt, ta được MH=8 cm
Áp dụng Pytago trong tam giác vuông AMH: AH2= AM2 - MH2 = 102 - 82= 36 ----> AH=6 cm
có AM=MC ; IB=IC ---> MI=1/2AB=1/2 .24 =12 cm( đường TB)
Từ I kẻ IK vuông góc AB
có MI// AB( MI là đường trung bình) ; IK//MK (cùng vuông góc AB)
---> MIKH là hình bình hành
---> MI=HK=12 cm; MH=IK=8 cm
BK= AB-AH-HK = 24-6-12=6 cm
Xét tam giác AMH và tam giác BIK:
AH=BK=6
góc AHM= góc BKI= 90O
MH=IK=8
----> tam giác AMH=tam giác BIK(c.g.c)
----> góc MAH= góc IBK (cặp góc tương ứng) hay góc CAB= góc CBA
----> tam giác ABC cân tại C
b) có AM=MC=AC/2=10 cm ; IB=IC= BC/2 ; mà AC=BC (tam giáccân)
----> AM=MC=IB=IC=10 cm
Kéo dài CO cắt AB tại D
tam giác AOC có OA=OC (bán kính) --> tam giác AOC cân tại O
có OM là trung tuyến ---> OM vuông góc AC hay góc OMC=90o
Tương tự với tam giác OCB được OI vuông góc BC hay góc OIC=90o
Xét tam giác vuông OMC và tam giác vuông OIC:
MC=IC=10cm
OC cạnh chung
--->tam giác OMC = tam giác OIC (ch.cgv)
--> góc MCO= góc ICO ---> CO hay CD là phân giác góc ACB của tam giác cân ABC --->
CD vuông góc AB hay góc ADC=90oAD=BD=AB/2 = 12 cm
Theo Pytago trong tam giác ACD: CD2= AC2-AD2 = 202-122 =256 ---> CD=16 cm
Đặt OC=OA=X --> OD= CD-OC = 16 - X
Theo Pytago tam giác AOD: AO2= OD2+AD2
<-->X2= (16-X)2 + 122
<--> 162 -32X + X2 +122 - X2=0
<--> 400 - 32X=0
<--> X= -400/-32= 12,5 cm
Vậy bán kính đường tròn bằng 12,5 cm
a) Áp dụng định lí py ta go trong \(\Delta\)ABC:\(\widehat{A}\)=1v
BC2= AB2+AC2
=62+82
=>BC=10
áp dụng hệ thức lượng giữa cạnh và góc trong \(\Delta\)ABC:
\(\dfrac{1}{h^2}=\dfrac{1}{b^2}+\dfrac{1}{c^2}\) => \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{1}{6^2}+\dfrac{1}{8^2}=\dfrac{25}{576}\)
=>AH=23,04
Ta có :
AB2=BC2.BH2
=>BH=\(\dfrac{AB^2}{BC}\)=\(\dfrac{6^2}{10}=3,6\)
BC=BH+HC
=>HC=BC-BH=10-3,6=6,4
hứng minh được AEB \backsim AFCAEB∽AFC, từ đó có \dfrac{AE}{AB} = \dfrac{AF}{AC}t.AE phần AB=AF phần AC
Ta có: \Delta AEF\backsim\Delta ABCΔAEF∽ΔABC (g.c.g)
b, từ câu a) suy ra EF phần BC=AE phần AB=cos A=cos60 độ =1 phần 2
=> BC=10cm
c) Saef phần Sabc=(AE phần AB)^2=cos^2 A=1 phần 4 => SAEF =1 phần 4 SABC=25cm^2
1.
Chứng minh được \widehat{CEB} = \widehat{BDC} = 90^{\circ}CEB=BDC=90∘.
Suy ra 44 điểm B,E, D, CB,E,D,C cùng thuộc đường tròn đường kính CBCB nên tứ giác BCDEBCDE nội tiếp.
Có tứ giác BCDEBCDE nội tiếp nên \widehat{DCE} = \widehat{DBE}DCE=DBE (22 góc nội tiếp cùng chắn cung DEDE) hay \widehat{ACQ} = \widehat{ABP}ACQ=ABP.
Trong đường tròn tâm (O)(O), ta có \widehat{ACQ}ACQ là góc nội tiếp chắn cung AQAQ và \widehat{ABP}ABP nội tiếp chắn cung APAP
\Rightarrow \overset{\frown}{AQ}=\overset{\frown}{AP}⇒AQ⌢=AP⌢.
2.
(O)(O) có \overset{\frown}{AQ}=\overset{\frown}{AP}AQ⌢=AP⌢ nên \widehat{ABP} = \widehat{ABQ}ABP=ABQ hay \widehat{HBE} = \widehat{QBE}HBE=QBE.
Ta chứng minh được BEBE vừa là đường cao, vừa là phân giác của tam giác HBQHBQ nên EE là trung điểm của HQHQ.
Chứng minh tương tự DD là trung điểm của HPHP \Rightarrow DE⇒DE là đường trung bình của tam giác HPQHPQ \Rightarrow DE // PQ⇒DE//PQ (1).
Do \overset{\frown}{AQ}=\overset{\frown}{AP}AQ⌢=AP⌢ nên AA là điểm chính giữa cung PQPQ \Rightarrow OA \perp PQ⇒OA⊥PQ (2).
Từ (1) và (2) suy ra OA \perp DEOA⊥DE.
3.
Kẻ đường kính CFCF của đường tròn tâm (O)(O), chứng minh tứ giác ADHEADHE nội tiếp đường tròn đường kính AHAH.
Chứng minh tứ giác AFBHAFBH là hình bình hành, suy ra BF=AHBF=AH.
Trong đường tròn (O)(O) có \widehat{CAB} = \widehat{CFB} = 60^{\circ}CAB=CFB=60∘ (2 góc nội tiếp cùng chắn cung BCBC). Chỉ ra tam giác BCFBCF vuông tại BB và áp dụng hệ thức giữa cạnh và góc ta được BF=CF. \cos 60^{\circ} =R=6BF=CF.cos60∘=R=6 cm.
Đường tròn ngoại tiếp tứ giác ADHEADHE cũng là đường tròn ngoại tiếp tam giác ADEADE.
Gọi rr là bán kính đường tròn ngoại tiếp tam giác ADEADE.
Suy ra 2r=AH=BF=62r=AH=BF=6 cm.
Vậy r=3r=3 cm.
Bài làm :
a) Ta có :
\(\widehat{ACB}\text{ là góc nội tếp chắn nửa đường tròn}\)
\(\Rightarrow\widehat{ACB}=90^o\Rightarrow\widehat{ACM}=180^o-\widehat{ACB}=90^o\)
Từ đó ; ta có :
\(\widehat{ACM}+\widehat{AHM}=90+90=180^o\)
=> Tứ giác AHMC là tứ giác nội tiếp đường tròn vì có 2 góc đối diện = 180 độ
=> Điều phải chứng minh
b) Theo phần a : Tứ giác AHMC là tứ giác nội tiếp
\(\Rightarrow\widehat{AMH}=\widehat{ACH}\left(1\right)\)
Xét đường tròn (O) : Góc ADC và góc ABC đều là 2 góc nội tiếp cùng chắn cung AC
\(\Rightarrow\widehat{ADC}=\widehat{ABC}\left(2\right)\)
Vì CD⊥AB ; MH⊥AB
=> CD//MH
=>∠ADC = ∠AMH ( 2góc so le trong ) (3)
Từ (1) ; (2) ; (3)
\(\Rightarrow\widehat{ABC}=\widehat{ACH}\)
=> Điều phải chứng minh
c)∠AOC = 45o
=>∠COB = 180 - 45 = 135o
\(\Rightarrow S_{OCB}=\frac{\pi.R^2.n}{360}=\frac{\pi.2^2.135}{360}=\frac{3}{2}\pi\left(cm^2\right)\)
a) Xét tứ giác AHMC có
góc ACM + góc AHM = 180 độ
Vậy tứ giác AHMC nội tiếp
A B C D M N E F I
Vì: FBM=FAM=45 độ nên BFMA là tứ giác nội tiếp
tương tự có đpcm
b, ta có:
MFN=DAB=90
NEM=BCD=90
=> nội tiếp
c, theo câu b ta có:
MNB=BEC=BNC nên: NB là phân giác góc INC
thấy ngay H là trực tâm tam giác BMN nên: BI vuông góc MN
do đó áp dụng tính chất đường phân giác ta được BI=BC=a.
Chứng minh góc EBN = góc ECN = 450
=> Tứ giác BENC nội tiếp (đpcm)
xét tam giác ABC cân tại A
có AM là trung tuyến
=> AM là đg cao
ta có góc AMB =90 độ
ADB=90 độ(BD vg góc AC)
=>Tứ giác ABMD nội tiếp
xét tam giác BDM có N,I lần lượt là trg điểm MB,BD
=> NI là đtb tam giác BMD
=>IN//DM=> góc INM= DMC
=> góc DMC =BAK
ta có gócINM=BAK cùng= DMC
=> tứ giác ABNK nội tiếp
b) xét tam giác CNK, CAB có NCK chung
góc CNK= BAC(cmt)
=> 2 tam giác CNK, CAB đồng dạng(g.g)
=> CK/cb= CN/AC
=> AC.CK=BC.CN
mà CN=MN+MC= BC/4+BC/2=3BC/4
nên AC.CK=3.BC^2/4=> BC^2= 4/3AC.CK
a) xét tam giác ABC cân tại A
AM là đường trung tuyến => AM là đường cao
ta có : AMB = 90 độ
ADB = 90 độ ( BD vuông góc với AC)
=> tứ giác ABMD nội tiếp đường tròn
xét tam giác BDM có lần lượt N, I là trung điểm của MB và BD
=> NI là đường trung bình của tam giác BDM
=> IN//DM
=> +INM = DMC
+ DMC = BAK
=> INM = BAK
=> tứ giác ABNK nội tiếp.
b) xét tam giác CNK, CAB có NCK chung
góc CNK = BAC
=> tam giác CNK đồng dạng với tam giác CAB
=> CK/CB=CN/AC
=> AC.CK=BC.CN
mà CN = MN+MC= BC/4 + BC/2=3BC/4
nên AC.CK=3BC^2/4=> BC2=34CA.CK
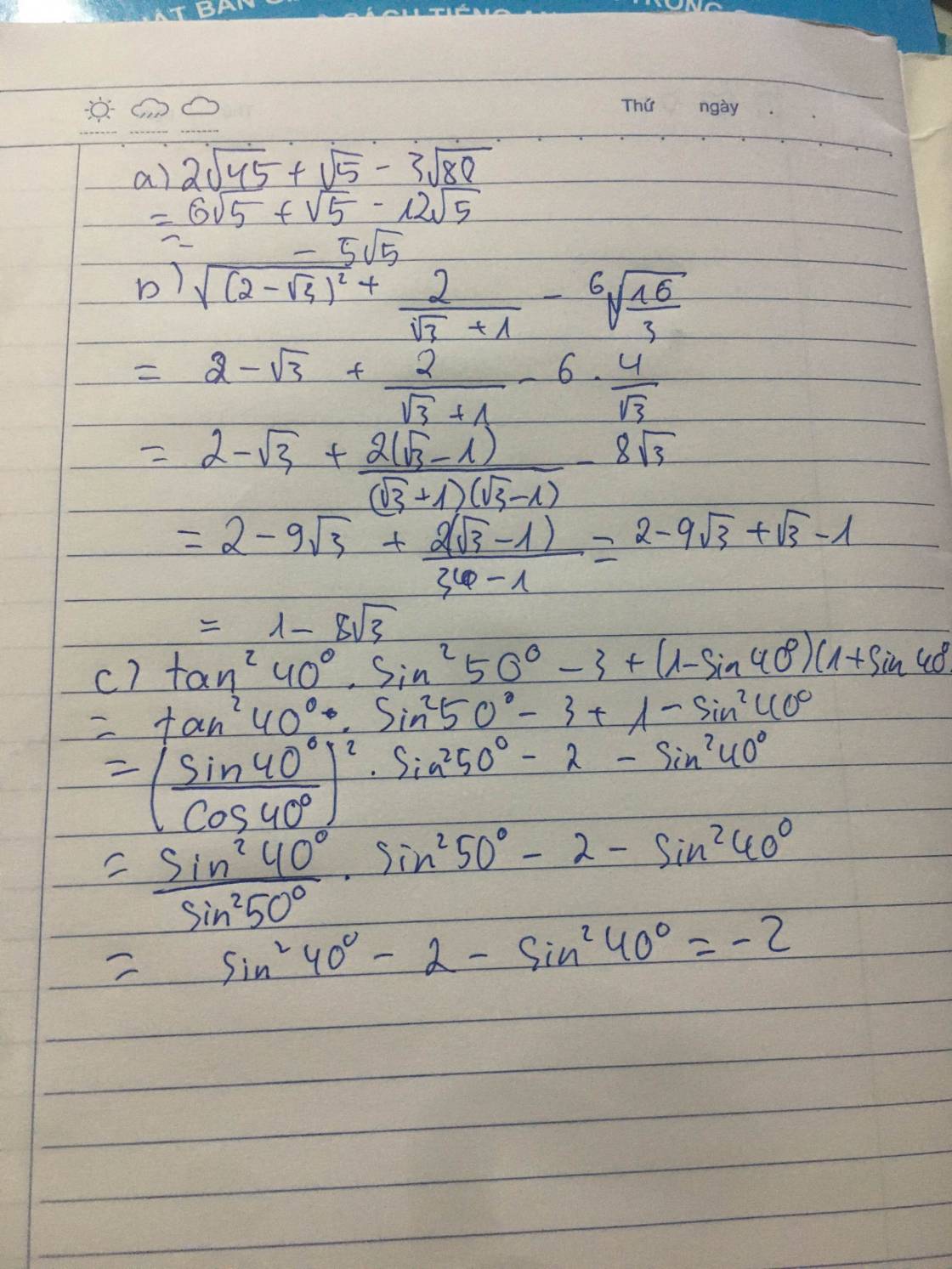
1) sin35⁰ = cos(90⁰ - 35⁰) = cos55⁰
Vậy sin35⁰ = cos55⁰
tan35⁰ = cot(90⁰ - 35⁰) = cot55⁰
Vậy tan35⁰ = cot55⁰
2) ∆ABC vuông tại A (gt)
⇒ AB = BC.cosB
= 20.cos36⁰
≈ 16,18 (cm)