Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1:
a) \(\dfrac{-15}{17}\) và \(\dfrac{-19}{21}\)
Ta có: \(\dfrac{-15}{17}=-1+\dfrac{2}{17}\); \(\dfrac{-19}{21}=-1+\dfrac{2}{21}\)
Vì \(\dfrac{2}{17}>\dfrac{2}{21}\)
Do đó: \(\dfrac{-15}{17}>\dfrac{19}{-23}\)
b) \(\dfrac{-13}{19}\) và \(\dfrac{19}{-23}\)
Ta có: \(\dfrac{19}{23}>\dfrac{19}{25}\); \(\dfrac{13}{19}=1-\dfrac{6}{19}\); \(\dfrac{19}{25}=1-\dfrac{6}{25}\)
mà \(\dfrac{6}{19}>\dfrac{6}{25}\) \(\Rightarrow\dfrac{13}{19}< \dfrac{19}{25}< \dfrac{19}{23}\)
Vì \(\dfrac{13}{19}< \dfrac{19}{23}\Rightarrow\dfrac{-13}{19}>\dfrac{19}{-23}\)
c) \(\dfrac{-24}{35}\) và \(\dfrac{-19}{30}\)
Ta có: \(\dfrac{-24}{35}=-1+\dfrac{19}{35}\);\(\dfrac{-19}{30}=-1+\dfrac{11}{30}\)
Vì \(\dfrac{11}{35}< \dfrac{11}{30}\)
Do đó: \(\dfrac{-24}{35}< \dfrac{-19}{30}\)
d) \(\dfrac{-1941}{1931}\) và \(\dfrac{-2011}{2001}\); \(\dfrac{-2011}{2001}=-1+\dfrac{10}{2001}\)
Vì \(\dfrac{10}{1931}< \dfrac{10}{1001}\)
Do đó: \(\dfrac{-1941}{1931}< \dfrac{-2011}{2001}\)
Ta có: \(\dfrac{-1941}{1931}=-1+\dfrac{10}{1931}\)
Sorry câu d mình viết ngược:
Làm lại:
d) \(\dfrac{-1941}{1931}\) và \(\dfrac{-2011}{2001}\)
Ta có: \(\dfrac{-1941}{1931}=-1+\dfrac{10}{1931};\)
\(\dfrac{-2011}{2001}=-1+\dfrac{10}{2001}\)
Vì \(\dfrac{10}{1931}< \dfrac{10}{1001}\)
Do đó: \(\dfrac{-1941}{1931}< \dfrac{-2011}{2001}\)

Dấu " / " là phân số nhé
a) 5/-4 . 16/25 + -5/4 . 9/25
= -5/4 . 16/25 + -5/4 . 9/25
= -5/4 . ( 16/25 + 9/25 )
= -5/4 . 1
= -5/4
b) 4 11/23 - 9/14 + 2 12/23 - 5/4
= 103/23 - 9/14 + 58/23 - 5/4
= 103/23 + 58/23 - 9/14 - 5/4
= 7 - 9/14 - 5/4
= 143/28
c) 2 13/27 - 7/15 + 3 14/27 - 8/15
= 67/27 - 7/15 + 95/27 - 8/15
= 67/27 + 95/27 - 7/15 - 8/15
= 6 - 7/15 - 8/15
= 5

2) Tinh nhanh:
a) \(\dfrac{5}{23}\) . \(\dfrac{17}{26}\) + \(\dfrac{5}{23}\) . \(\dfrac{10}{26}\) - \(\dfrac{5}{23}\)
= \(\dfrac{5}{23}\) . \(\left(\dfrac{17}{26}+\dfrac{10}{26}-1\right)\)
= \(\dfrac{5}{23}\) . \(\left(\dfrac{27}{26}-1\right)\) = \(\dfrac{5}{23}\) . \(\dfrac{1}{26}\)
= \(\dfrac{5}{598}\)
b) \(\dfrac{1}{7}.\dfrac{5}{9}+\dfrac{5}{9}.\dfrac{2}{7}+\dfrac{5}{9}.\dfrac{1}{7}+\dfrac{5}{9}.\dfrac{3}{7}\)
= \(\dfrac{5}{9}.\left(\dfrac{1}{7}+\dfrac{2}{7}+\dfrac{1}{7}+\dfrac{3}{7}\right)\)
= \(\dfrac{5}{9}\) . 1= \(\dfrac{5}{9}\)

Bài 1: Tính ( hợp lý nếu có thể )
\(A=\dfrac{-3}{8}+\dfrac{12}{25}+\dfrac{5}{-8}+\dfrac{2}{-5}+\dfrac{13}{25}\)
\(=\left(\dfrac{-3}{8}+\dfrac{5}{-8}\right)+\left(\dfrac{12}{25}+\dfrac{13}{25}\right)+\dfrac{2}{-5}\)
\(=-1+1+\dfrac{2}{-5}\)
\(=0+\dfrac{2}{-5}\)
\(=\dfrac{2}{-5}\)
\(B=\dfrac{-3}{15}+\left(\dfrac{2}{3}+\dfrac{3}{15}\right)\)
\(=\left(\dfrac{-3}{15}+\dfrac{3}{15}\right)+\dfrac{2}{3}\)
\(=0+\dfrac{2}{3}\)
\(=\dfrac{2}{3}\)
\(C=\dfrac{-5}{21}+\left(\dfrac{-16}{21}+1\right)\)
\(=\left(\dfrac{-5}{21}+\dfrac{-16}{21}\right)+1\)
\(=-1+1\)
\(=0\)
\(D=\left(\dfrac{-1}{6}+\dfrac{5}{-12}\right)+\dfrac{7}{12}\)
\(=\left(\dfrac{5}{-12}+\dfrac{7}{12}\right)+\dfrac{-1}{6}\)
\(=\dfrac{1}{6}+\dfrac{-1}{6}\)
\(=0\)
Bài 2: Tìm x,biết:
a) \(x+\dfrac{2}{3}=\dfrac{4}{5}\)
\(x=\dfrac{4}{5}-\dfrac{2}{3}\)
\(x=\dfrac{2}{15}\)
Vậy \(x=\dfrac{2}{15}\)
b) \(x-\dfrac{2}{3}=\dfrac{7}{21}\)
\(\Rightarrow x-\dfrac{2}{3}=\dfrac{1}{3}\)
\(x=\dfrac{1}{3}+\dfrac{2}{3}\)
\(x=\dfrac{3}{3}=1\)
Vậy \(x=1\)
c) sai đề hay sao ấy bạn.bỏ dấu - ở x thì đúng đề.mk giải luôn nha!
\(x-\dfrac{3}{4}=\dfrac{-8}{11}\)
\(x=\dfrac{-8}{11}+\dfrac{3}{4}\)
\(x=\dfrac{1}{44}\)
Vậy \(x=\dfrac{1}{44}\)
d) \(\dfrac{11}{12}-\left(\dfrac{2}{5}+x\right)=\dfrac{2}{3}\)
\(\dfrac{2}{5}+x=\dfrac{11}{12}-\dfrac{2}{3}\)
\(\dfrac{2}{5}+x=\dfrac{1}{4}\)
\(x=\dfrac{1}{4}-\dfrac{2}{5}\)
\(x=-\dfrac{3}{20}\)
Vậy \(x=-\dfrac{3}{20}\)

a , \(\left(\dfrac{-2}{3}+1\dfrac{1}{4}-\dfrac{1}{6}\right):\dfrac{-24}{10}\)
=\(\left(\dfrac{-2}{3}+\dfrac{5}{4}-\dfrac{1}{6}\right):\dfrac{-12}{5}\)
=\(\left(\dfrac{-8}{12}+\dfrac{15}{12}-\dfrac{2}{12}\right)\cdot\dfrac{-5}{12}\)
=\(\dfrac{5}{12}\cdot\dfrac{-5}{12}=\dfrac{-25}{144}\)
b , \(\dfrac{13}{15}\cdot0,25\cdot3+\left(\dfrac{8}{15}-1\dfrac{19}{60}\right)1\dfrac{23}{24}\)
=\(\dfrac{13}{15}\cdot\dfrac{1}{4}\cdot3+\left(\dfrac{8}{15}-\dfrac{79}{60}\right)\cdot\dfrac{57}{24}\)
=\(\dfrac{13}{20}-\dfrac{47}{60}\cdot\dfrac{57}{24}\)
=\(\dfrac{13}{20}-\dfrac{893}{480}=\dfrac{312}{480}-\dfrac{893}{480}=\dfrac{-581}{480}\)
c , \(\left(\dfrac{12}{32}+\dfrac{5}{-20}-\dfrac{10}{24}\right):\dfrac{2}{3}\)
=\(\left(\dfrac{180}{480}-\dfrac{120}{480}-\dfrac{200}{480}\right)\cdot\dfrac{3}{2}\)
= \(\dfrac{-7}{24}\cdot\dfrac{3}{2}=\dfrac{-7}{16}\)
d , \(4\dfrac{1}{2}:\left(2,5-3\dfrac{3}{4}\right)+\left(-\dfrac{1}{2}\right)\)
=\(\dfrac{9}{2}:\left(\dfrac{5}{2}-\dfrac{15}{4}\right)-\dfrac{1}{2}\)
=\(\dfrac{9}{2}:\dfrac{-5}{4}-\dfrac{1}{2}=\dfrac{9}{2}\cdot\dfrac{-4}{5}-\dfrac{1}{2}=\dfrac{-18}{5}-\dfrac{1}{2}=\dfrac{-41}{10}\)
e , \(\dfrac{-5}{2}:\left(\dfrac{3}{4}-\dfrac{1}{2}\right)=\dfrac{-5}{2}\left(\dfrac{3}{4}-\dfrac{2}{4}\right)\)
=\(\dfrac{-5}{2}:\dfrac{1}{4}=\dfrac{-5}{2}\cdot4=-10\)

a) \(\dfrac{-1}{-4}\)=\(\dfrac{1}{4}>0\)
\(\dfrac{3}{-4}< 0\)
\(\Rightarrow\dfrac{1}{4}>\dfrac{3}{-4}hay\dfrac{-1}{-4}>\dfrac{3}{-4}\)
b) Ta có:
\(\dfrac{15}{17}=1-\dfrac{2}{17}\\ \)
\(\dfrac{25}{27}=1-\dfrac{2}{27}\\ \\ \)
Mà \(\dfrac{2}{17}>\dfrac{2}{27}\left(17< 27\right)\)
\(\Rightarrow1-\dfrac{2}{17}< 1-\dfrac{2}{27}\)hay \(\dfrac{15}{17}< \dfrac{25}{27}\)

tính chất trên gọi là tính chất bắc cầu, ta so sánh hai phân số với một số (phân số) thứ 3.

mình ghi nhầm nên các bạn cứ hết hai phân số là một câu nhé ví dụ như \(\dfrac{-5}{8}\):\(\dfrac{15}{4}\)

a: \(=\dfrac{-8-38}{5}=\dfrac{-46}{5}\)
b: \(=\dfrac{-5}{7}\left(\dfrac{25}{1}-24-\dfrac{4}{7}\right)+\dfrac{46}{3}\cdot\dfrac{-1}{23}\)
\(=\dfrac{-5}{7}\cdot\dfrac{3}{7}+\dfrac{-2}{3}\)
=-15/49-2/3=-143/147

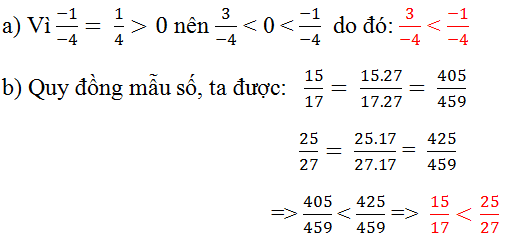
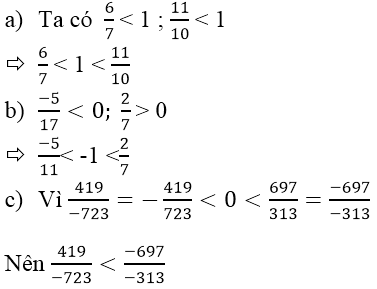
\(a,\dfrac{-15}{17}=-1+\dfrac{2}{17}\\ -\dfrac{19}{21}=-1+\dfrac{2}{21}\\ Vì:\dfrac{2}{17}>\dfrac{2}{21}\Rightarrow-1+\dfrac{2}{17}>-1+\dfrac{2}{21}\Rightarrow-\dfrac{15}{17}>-\dfrac{19}{21}\\ b,-\dfrac{24}{35}=-1+\dfrac{11}{35};-\dfrac{19}{30}=-1+\dfrac{11}{30}\\ Vì:\dfrac{11}{35}< \dfrac{11}{30}\Rightarrow-1+\dfrac{11}{35}< -1+\dfrac{11}{30}\\ \Rightarrow-\dfrac{24}{35}< -\dfrac{19}{30}\)