PG
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
UI
11
3 tháng 4 2020
Ta có :1996! = 1.2.3 . ... . 1995 . 1996
: 1995! = 1.2.3 . ... . 1995
=> 1996! > 1995 !
=> \(\sqrt[1995]{1996}>\sqrt[1995]{1995!}\)
NT
2
1 tháng 11 2017
a,hay \(\left(1995\cdot1997\right)^n\)và \(\left(1996\cdot1996\right)^n\)
hay so sánh \(1995\cdot1997\)và \(1996\cdot1996\)
ta có 1995*1997=1995*(1996+1)=1995*1996+1995
1996*1996=1996*(1995+1)=1996*1995+1996
vì 1995<1996 => \(\left(1995\cdot1997\right)^n\)<\(\left(1996\cdot1996\right)^n\)
17 tháng 8 2021
1, A=\(\left(1-\dfrac{2\sqrt{a}}{a+1}\right):\left(\dfrac{1}{\sqrt{a}+1}-\dfrac{2\sqrt{a}}{a\sqrt{a}+\sqrt{a}+a+1}\right)\)
ĐKXĐ: a≥0
A=\(\left(1-\dfrac{2\sqrt{a}}{a+1}\right):\left(\dfrac{1}{\sqrt{a}+1}-\dfrac{2\sqrt{a}}{\sqrt{a}\left(a+1\right)+1\left(a+1\right)}\right)\)
A=\(\left(\dfrac{a+1}{a+1}-\dfrac{2\sqrt{a}}{a+1}\right):\left(\dfrac{a+1}{\left(\sqrt{a}+1\right)\left(a+1\right)}-\dfrac{2\sqrt{a}}{\left(\sqrt{a}+1\right)\left(a+1\right)}\right)\)
A=\(\left(\dfrac{a+1-2\sqrt{a}}{a+1}\right):\left(\dfrac{a+1-2\sqrt{a}}{\left(\sqrt{a}+1\right)\left(a+1\right)}\right)\)
A=\(\left(\dfrac{a+1-2\sqrt{a}}{a+1}\right).\left(\dfrac{\left(a+1\right)\left(\sqrt{a}+1\right)}{a+1-2\sqrt{a}}\right)\)
A=\(\sqrt{a}+1\)
Vậy A=\(\sqrt{a}+1\)
2, a=1996-2\(\sqrt{1995}\)
a=\(1995-2\sqrt{1995}+1\)
a=\(\left(\sqrt{1995}-1\right)^2\) (TMĐKXĐ)
thay a=\(\left(\sqrt{1995}-1\right)^2\) vào A ta có:
A=\(\sqrt{\left(\sqrt{1995}-1\right)^2}+1\)
A=\(\sqrt{1995}\)
Vậy a=1996-2\(\sqrt{1995}\) thì A=\(\sqrt{1995}\)
VT
17 tháng 6 2018
ĐKXĐ: a ≥ 0
a) Ta có:
P = \(\left(1-\dfrac{2\sqrt{a}}{a+1}\right):\left(\dfrac{1}{\sqrt{a}+1}-\dfrac{2\sqrt{a}}{a\sqrt{a}+\sqrt{a}+a+1}\right)\)
= \(\dfrac{a-2\sqrt{a}+1}{a+1}:\left(\dfrac{1}{\sqrt{a}+1}-\dfrac{2\sqrt{a}}{\left(\sqrt{a}+1\right)\left(a+1\right)}\right)\)
= \(\dfrac{\left(\sqrt{a}-1\right)^2}{a+1}:\dfrac{a-2\sqrt{a}+1}{\left(\sqrt{a}+1\right)\left(a+1\right)}\)
= \(\dfrac{\left(\sqrt{a}-1\right)^2}{a+1}.\dfrac{\left(\sqrt{a}+1\right)\left(a+1\right)}{\left(\sqrt{a}-1\right)^2}\)
Vậy P = \(\sqrt{a}+1\) với a ≥ 0
b) Ta có: a = \(1996-2\sqrt{1995}\) = \(\left(\sqrt{1995}-1\right)^2\) (TMĐK)
⇒ \(\sqrt{a}=\sqrt{1995}-1\). Thay vào P ta được
P = \(\sqrt{1995}-1+1=\sqrt{1995}\)
Vậy P = \(\sqrt{1995}\) khi a = \(1996-2\sqrt{1995}\)
12 tháng 11 2018
c) \(\sqrt{x-4}-\sqrt{x+11}=-3\) (đk \(x\ge4\))
\(\Leftrightarrow\sqrt{x-4}+3=\sqrt{x+11}\)
\(\Leftrightarrow\left(\sqrt{x-4}+3\right)^2=x+11\)
\(\Leftrightarrow x-4+6\sqrt{x-4}+9=x+11\)
\(\Leftrightarrow6\sqrt{x-4}=6\)
\(\Leftrightarrow\sqrt{x-4}=1\)
\(\Leftrightarrow x-4=1\)
\(\Leftrightarrow x=5\)
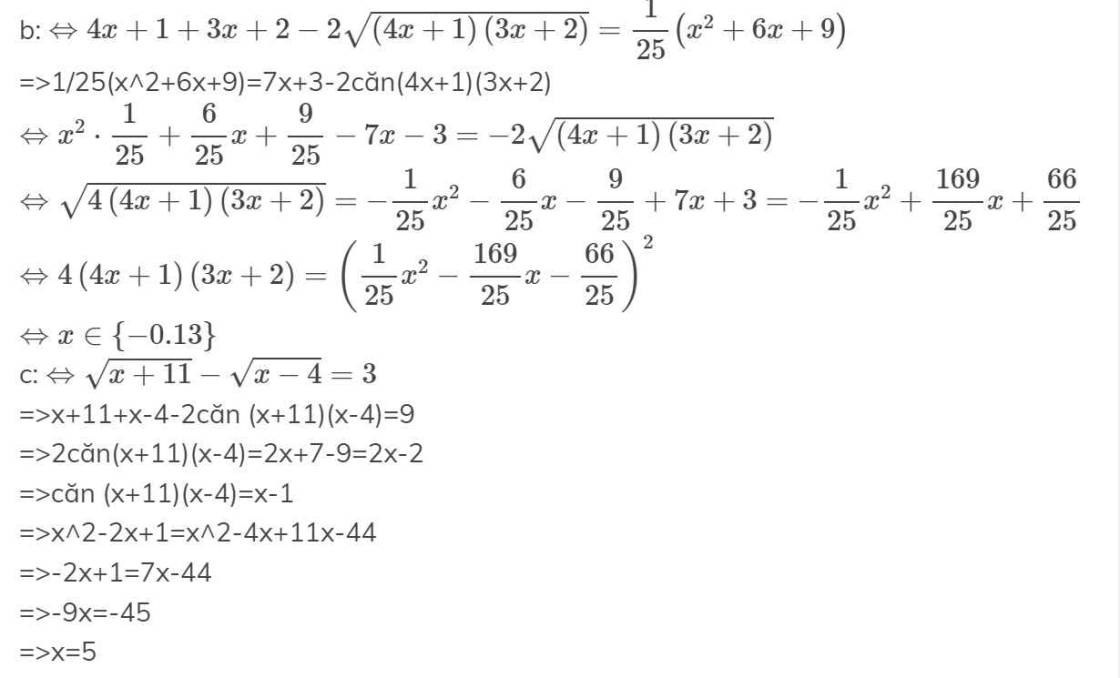
ta có bđt \(\left(\frac{a+b}{2}\right)^n\le\frac{a^n+b^n}{2}\) với mọi \(a+b\ge0\) và \(n\inℝ\)
\(1+\sqrt[1995]{1995}=2\sqrt[1995]{\left(\frac{1+\sqrt[1995]{1995}}{2}\right)^{1995}}\le2\sqrt[1995]{\frac{1+1995}{2}}=2\sqrt[1995]{\frac{1996}{2}}\)
\(=\sqrt[1995]{2^{1994}.1996}=\sqrt[1995]{2.2...2.1996}< \sqrt[1995]{2.3...1995.1996}=\sqrt[1995]{1996!}\)