
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


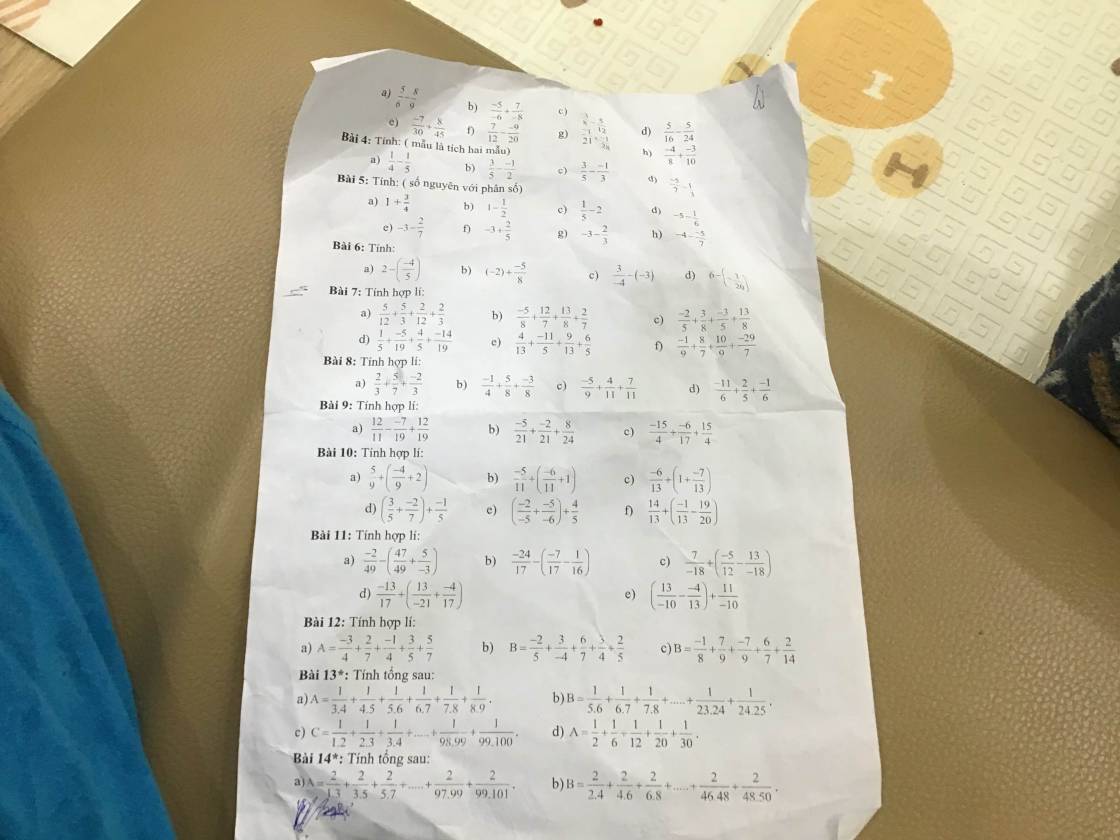
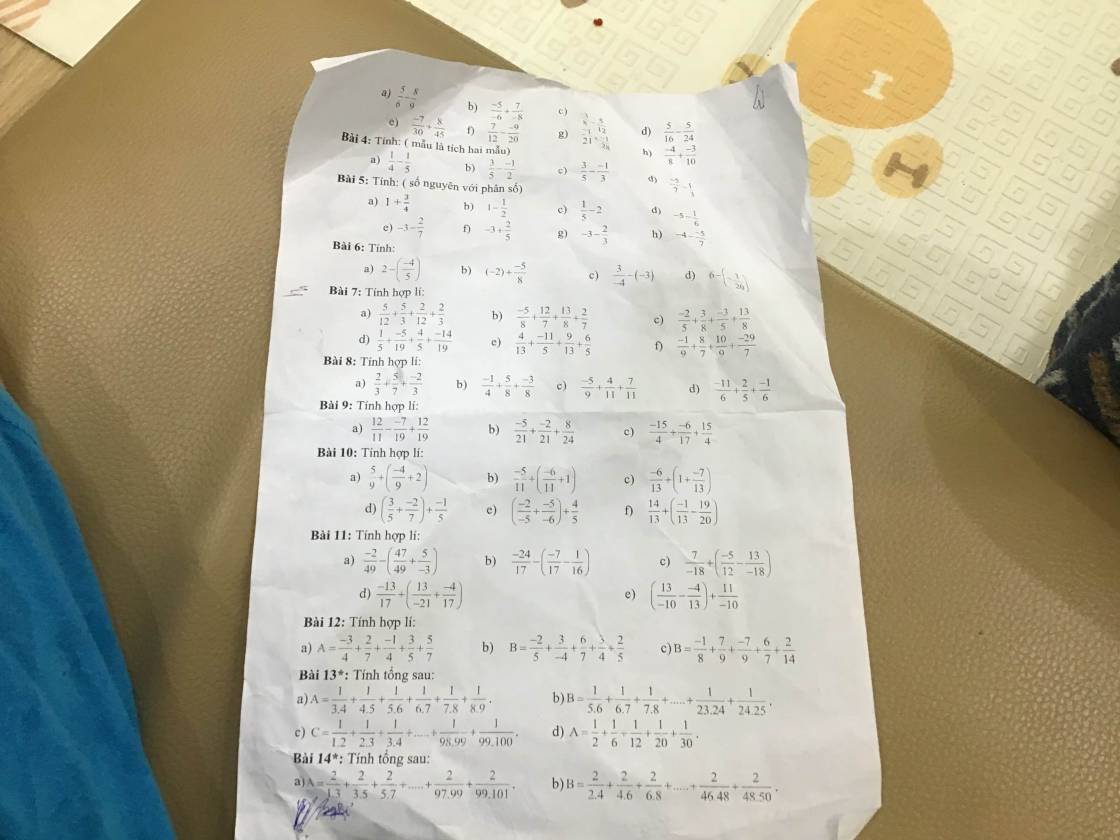
Bài 4:
a; \(\dfrac{1}{4}\) - \(\dfrac{1}{5}\) = \(\dfrac{5}{20}\) - \(\dfrac{4}{20}\) = \(\dfrac{1}{20}\)
b; \(\dfrac{3}{5}\) - \(\dfrac{-1}{2}\) = \(\dfrac{6}{10}\) + \(\dfrac{5}{10}\) = \(\dfrac{11}{10}\)
c; \(\dfrac{3}{5}\) - \(\dfrac{-1}{3}\) = \(\dfrac{9}{15}\) + \(\dfrac{5}{15}\) = \(\dfrac{14}{15}\)
d; \(\dfrac{-5}{7}\) - \(\dfrac{1}{3}\)= \(\dfrac{-15}{21}\) - \(\dfrac{7}{21}\)= \(\dfrac{-22}{21}\)
Bài 5
a; 1 + \(\dfrac{3}{4}\) = \(\dfrac{4}{4}\) + \(\dfrac{3}{4}\) = \(\dfrac{7}{4}\) b; 1 - \(\dfrac{1}{2}\) = \(\dfrac{2}{2}\) - \(\dfrac{1}{2}\) = \(\dfrac{1}{2}\)
c; \(\dfrac{1}{5}\) - 2 = \(\dfrac{1}{5}\) - \(\dfrac{10}{5}\) = \(\dfrac{-9}{5}\) d; -5 - \(\dfrac{1}{6}\) = \(\dfrac{-30}{6}\) - \(\dfrac{1}{6}\) = \(\dfrac{-31}{6}\)
e; - 3 - \(\dfrac{2}{7}\)= \(\dfrac{-21}{7}\) - \(\dfrac{2}{7}\)= \(\dfrac{-23}{7}\) f; - 3 + \(\dfrac{2}{5}\) = \(\dfrac{-15}{5}\) + \(\dfrac{2}{5}\)= - \(\dfrac{13}{5}\)
g; - 3 - \(\dfrac{2}{3}\) = \(\dfrac{-9}{3}\) - \(\dfrac{2}{3}\) = \(\dfrac{-11}{3}\) h; - 4 - \(\dfrac{-5}{7}\) = \(\dfrac{-28}{7}\)+ \(\dfrac{5}{7}\) = - \(\dfrac{23}{7}\)

Có quá nhiều bài, thứ nhất em đăng tách ra, thứ hai chụp gần cận cho rõ, thứ ba em chỉ đăng bài cần giúp

\(a,MSC:180\\ Có:-5=\dfrac{-5.180}{180}=\dfrac{-900}{180};\dfrac{17}{-20}=\dfrac{17.\left(-9\right)}{\left(-9\right).\left(-20\right)}=\dfrac{-153}{180};\dfrac{-16}{9}=\dfrac{-16.20}{9.20}=\dfrac{-320}{180}\\ ---\\ b.MSC:75\\ Có:\dfrac{13}{-15}=\dfrac{13.\left(-5\right)}{\left(-15\right).\left(-5\right)}=\dfrac{-65}{75};\dfrac{-18}{25}=\dfrac{-18.3}{25.3}=\dfrac{-54}{75};-3=\dfrac{-3.75}{75}=\dfrac{-225}{75}\)

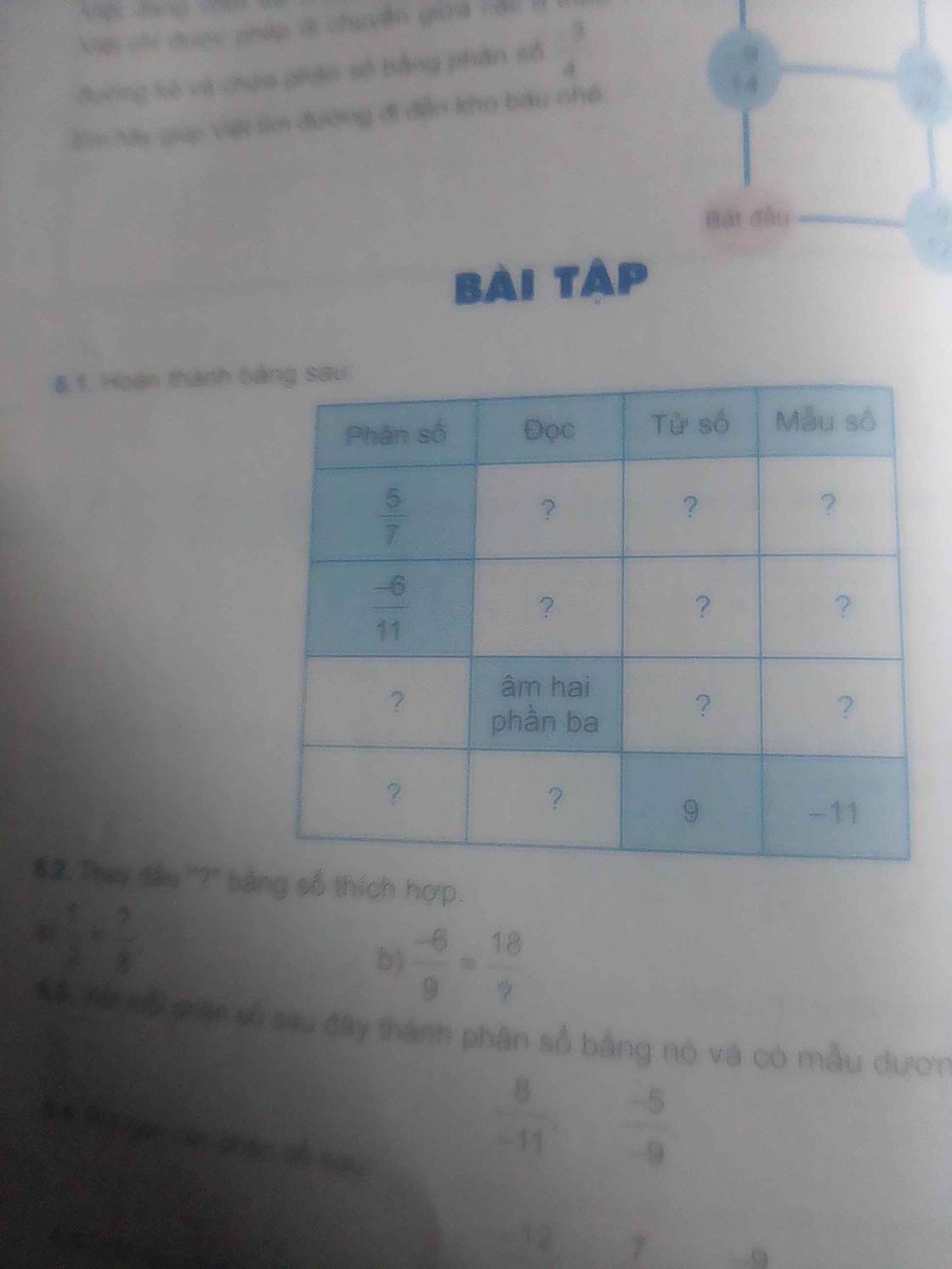
| Phân số | Đọc | Tử Số | Mẫu số |
| \(\dfrac{5}{7}\) | Năm phần bẩy | 5 | 7 |
| \(\dfrac{-6}{11}\) | âm sáu phần mười một | -6 | 11 |
| \(\dfrac{-2}{13}\) | âm hai phần ba | -2 | 13 |
| \(\dfrac{9}{-11}\) | chín phần âm mười một | 9 | -11 |


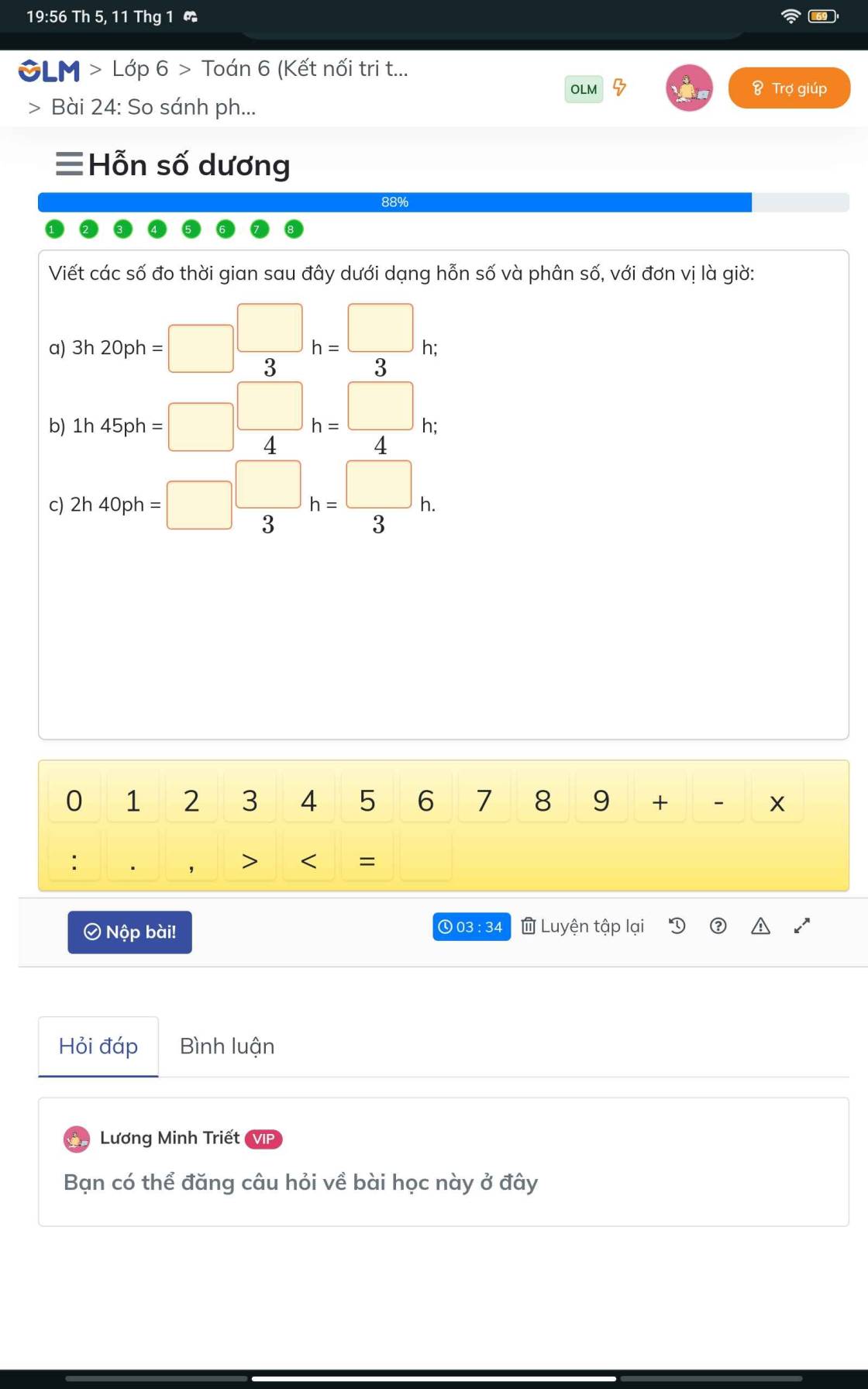
a) 3h 20ph = 3 và 1/3 = 10/3
b) 1h 45 ph = 1 và 3/4 = 7/4
c) 2h 40 ph = 2 và 2/3 = 8/3
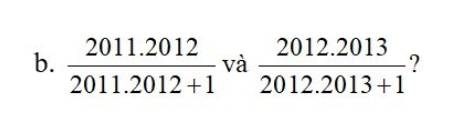

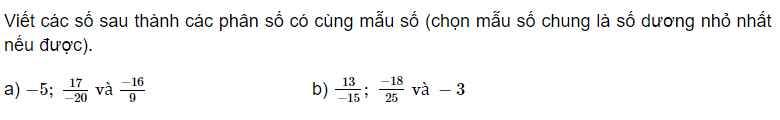
\(\dfrac{2011\cdot2012}{2011\cdot2012+1}=\dfrac{2011\cdot2012+1-1}{2011\cdot2012+1}=1-\dfrac{1}{2011\cdot2012+1}\)
\(\dfrac{2012\cdot2013}{2012\cdot2013+1}=\dfrac{2012\cdot2013+1-1}{2012\cdot2013+1}=1-\dfrac{1}{2012\cdot2013+1}\)
Ta có: \(2011\cdot2012< 2012\cdot2013\)
=>\(2011\cdot2012+1< 2012\cdot2013+1\)
=>\(\dfrac{1}{2011\cdot2012+1}>\dfrac{1}{2012\cdot2013+1}\)
=>\(-\dfrac{1}{2011\cdot2012+1}< \dfrac{-1}{2012\cdot2013+1}\)
=>\(\dfrac{-1}{2011\cdot2012}+1< \dfrac{-1}{2012\cdot2013+1}+1\)
=>\(\dfrac{2011\cdot2012}{2011\cdot2012+1}< \dfrac{2012\cdot2013}{2012\cdot2013+1}\)