Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(B=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2007}-\dfrac{1}{2008}=1-\dfrac{1}{2008}=\dfrac{2007}{2008}\)
b: \(Q=\dfrac{7}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{2009\cdot2011}\right)\)
\(=\dfrac{7}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2009}-\dfrac{1}{2011}\right)\)
\(=\dfrac{7}{2}\cdot\dfrac{2010}{2011}\simeq3,50\)

a) \(\dfrac{-1}{-4}\)=\(\dfrac{1}{4}>0\)
\(\dfrac{3}{-4}< 0\)
\(\Rightarrow\dfrac{1}{4}>\dfrac{3}{-4}hay\dfrac{-1}{-4}>\dfrac{3}{-4}\)
b) Ta có:
\(\dfrac{15}{17}=1-\dfrac{2}{17}\\ \)
\(\dfrac{25}{27}=1-\dfrac{2}{27}\\ \\ \)
Mà \(\dfrac{2}{17}>\dfrac{2}{27}\left(17< 27\right)\)
\(\Rightarrow1-\dfrac{2}{17}< 1-\dfrac{2}{27}\)hay \(\dfrac{15}{17}< \dfrac{25}{27}\)

\(\dfrac{2}{1.2}+\dfrac{2}{2.3}+\dfrac{2}{3.4}+...............+\dfrac{2}{2008.2009}\)
\(=2\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+................+\dfrac{1}{2008.2009}\right)\)
\(=2\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+.................+\dfrac{1}{2008}-\dfrac{1}{2009}\right)\)
\(=2\left(1-\dfrac{1}{2009}\right)\)
\(=2.\dfrac{2008}{2009}=\dfrac{4016}{2009}\)

a) \(\dfrac{3}{8}\) và \(\dfrac{5}{27}\)
Mẫu số chung là 216
Quy đồng:
\(\dfrac{3.27}{8.27}\)=\(\dfrac{81}{216}\) ; \(\dfrac{5.8}{27.8}\)=\(\dfrac{40}{216}\)
b)\(\dfrac{-2}{9}\) và \(\dfrac{4}{25}\)
Mẫu số chung là:225
Quy đồng:
\(\dfrac{-2.25}{9.25}\)=\(\dfrac{-50}{225}\) ; \(\dfrac{4.9}{25.9}\)=\(\dfrac{36}{225}\)
c)\(\dfrac{1}{15}\) và -6
Mẫu số chung là 15
Quy đồng:
\(\dfrac{1}{15}\) ;\(\dfrac{-6.15}{15}\)=\(\dfrac{-90}{15}\)

Vì 18/91 < 18/90 =1/5
23/114>23115=1/5
vậy 18/91<1/5<23/114
suy ra 18/91<23/114
vì 21/52=210/520
Mà 210/520=1-310/520
213/523=1-310/523
310/520>310/523
vậy 210/520<213/523
suy ra 21/52<213/523

a: 17/200>17/314
b: 11/54=22/108<22/37
c: 141/893=3/19
159/901=3/17
mà 3/19<3/17
nên 141/893<159/901
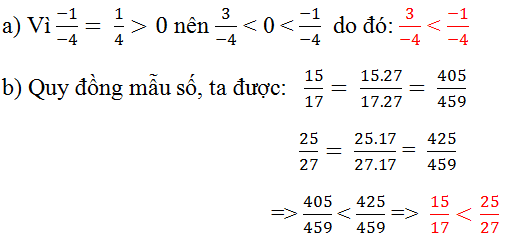
a)
\(A=\dfrac{2007.2008-1}{2007.2008}=1-\dfrac{1}{2007.2008}\)
\(B=\dfrac{2008.2009-1}{2008.2009}=1-\dfrac{1}{2008.2009}\)
\(A-B=\dfrac{1}{2008.2009}-\dfrac{1}{2007.2008}< 0\Rightarrow A< B\)
b)
\(\left\{{}\begin{matrix}A=\dfrac{25}{43}\\B=\dfrac{10}{27}\end{matrix}\right.\) ; \(\dfrac{A}{B}=\dfrac{25}{43}.\dfrac{27}{10}=\dfrac{5.27}{43.2}>\dfrac{54.2}{43.2}>1\Rightarrow A>B\)
thanks b