
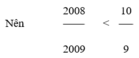
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

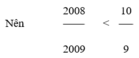

ta có:\(\frac{1}{2}=\frac{64}{128}>\frac{63}{128}\)
\(\frac{1}{2}=\frac{2008}{4016}< \frac{2008}{2009}\)
=> \(\frac{63}{128}< \frac{1}{2}< \frac{2008}{2009}\)
Vậy \(\frac{63}{128}< \frac{2008}{2009}\)

\(\frac{2009.2009+2008}{2009.2009+2009}=\frac{2009.2009+2009}{2009.2009+2009}-\frac{1}{2009.2009+2009}=1-\frac{1}{2009.2009+2009}\)
\(\frac{2009.2009+2009}{2009.2009+2010}=\frac{2009.2009+2010}{2009.2009+2010}-\frac{1}{2009.2009+2010}=1-\frac{1}{2009.2009+2010}\)
\(\text{Vì }2009.2009+2009<2009.2009+2010\text{ nên: }\frac{1}{2009.2009+2009}>\frac{1}{2009.2009+2010}\)
\(\text{Hay }1-\frac{1}{2009.2009+2009}<\frac{1}{2009.2009+2010}\)
\(\text{Vậy }\frac{2009.2009+2008}{2009.2009+2009}<\frac{2009.2009+2009}{2009.2009+2010}\)
\(\frac{2009.2009+2009}{2009.2009+2010}=\frac{2009.2009+2008+1}{2009.2009+2009+1}\)
Đặt 2009.2009+2008 là a; 2009.2009+2009 là b. Ta so sánh \(\frac{a}{b}\)và \(\frac{a+1}{b+1}\)
Qui đồng mẫu số 2 phân số trên
\(\frac{a}{b}=\frac{a\left(b+1\right)}{b\left(b+1\right)}=\frac{a.b+a}{b.\left(b+1\right)}\)
\(\frac{a+1}{b+1}=\frac{\left(a+1\right).b}{b\left(b+1\right)}=\frac{a.b+b}{b\left(b+1\right)}\)
Vì 2008 < 2009
=> 2009.2009+2008 < 2009.2009+2009
=> a < b
=> a.b+a < a.b+b
=> \(\frac{a.b+a}{b.\left(b+1\right)}<\frac{a.b+b}{b.\left(b+1\right)}\)
=> \(\frac{a}{b}<\frac{a+1}{b+1}\)
=> \(\frac{2009.2009+2008}{2009.2009+2009}<\frac{2009.2009+2009}{2009.2009+2010}\)

mỗi số hạng trong biểu thức A đều nhỏ hơn 1 mà có 15 số nên tổng A sẽ nhỏ hơn 15
ta thay tong tren <1+1+1+1+1+1+1+1+1+1+1+1+1+1+1
hay tong tren be hon 15

\(\frac{2007}{2008}\) và \(\frac{2008}{2009}\)
Phần bù của phân số \(\frac{2007}{2008}\)là: \(1\)- \(\frac{2007}{2008}\)= \(\frac{1}{2008}\)
Phần bù của phân số \(\frac{2008}{2009}\)là: \(1\)- \(\frac{2008}{2009}\)= \(\frac{1}{2009}\)
Phân số nào lớn hơn phân số kia trong phần bù thì phân số đó bé hơn
Vì \(\frac{1}{2008}\)> \(\frac{1}{2009}\)nên \(\frac{2007}{2008}\)< \(\frac{2008}{2009}\)
tk nhé

Vì 20009 x 2009 + 2008 < 2009 x 2009 + 2009
=>A < 1
Ta có: \(B=\frac{2009x2009+2009}{2008x2009+2010}=\frac{2009x\left(2008+1\right)+2009}{2008x2009+2010}=\frac{2008x2009+2009+2009}{2008x2009+2010}\)
\(B=\frac{2008x2009+4018}{2008x2009+2010}=\frac{2008x2009+2010+2008}{2008x2009+2010}=\frac{2008x2009+2010}{2008x2009+2010}+\frac{2008}{2008x2009+2010}\)
\(B=1+\frac{2008}{2008x2009+2010}>1\)
Mà A < 1
=>A < B