
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


10) \(\dfrac{\sqrt{160}-\sqrt{80}}{\sqrt{8}-\sqrt{2}}-\dfrac{\sqrt{40}-\sqrt{15}}{2\sqrt{2}-\sqrt{3}}\)
\(=\dfrac{4\sqrt{10}-4\sqrt{5}}{2\sqrt{2}-\sqrt{2}}-\dfrac{\sqrt{5}\left(\sqrt{8}-\sqrt{3}\right)}{\sqrt{8}-\sqrt{3}}\)
\(=\dfrac{4\sqrt{5}\left(\sqrt{2}-1\right)}{\sqrt{2}}-\sqrt{5}=\dfrac{\sqrt{80}\left(\sqrt{2}-1\right)}{\sqrt{2}}-\sqrt{5}\)
\(=\sqrt{40}\left(\sqrt{2}-1\right)-\sqrt{5}\)
\(=4\sqrt{5}-2\sqrt{10}-\sqrt{5}=3\sqrt{5}-2\sqrt{10}\)
\(=\dfrac{\sqrt{80}\left(\sqrt{2}-1\right)}{\sqrt{2}}-\sqrt{5}\)
=căn 40(căn 2-1)-căn 5
=4*căn 5-2*căn 10-căn 5
=3*căn 5-2*căn 10

a: Xét (O) có
ΔABC nội tiếp
AB là đường kính
Do đó: ΔABC vuông tại C

Gọi giá trị của chữ số sau khi xóa đi số 5 là x (với \(x>0;x\in N\))
Giá trị chữ số ban đầu: \(10x+5\)
Theo bài ra ta có pt:
\(10x+5-x=1796\)
\(\Rightarrow9x=1791\)
\(\Rightarrow x=199\)
Vậy chữ số đó là \(1995\)

Câu 8:
\(x^2+\left(2m+1\right)x-m^2=0\)
a=1; b=2m+1; c=-m2
Vì ac<=0 nên phương trình luôn có nghiệm
Theo đề, ta có: \(A=\left(x_1+x_2\right)^2-8x_1x_2\)
\(=\left(2m+1\right)^2-8\left(-m^2\right)\)
\(=4m^2+4m+1+8m^2=12m^2+4m+1\)
\(=12\left(m^2+\dfrac{1}{3}m+\dfrac{1}{12}\right)\)
\(=12\left(m^2+2\cdot m\cdot\dfrac{1}{6}+\dfrac{1}{36}+\dfrac{1}{18}\right)\)
\(=12\left(m+\dfrac{1}{6}\right)^2+\dfrac{2}{3}\ge\dfrac{2}{3}\forall m\)
Dấu '=' xảy ra khi m=-1/6

\(=\dfrac{\sqrt{x}+2-\sqrt{x}}{x-4}\cdot\dfrac{x+2}{1}=\dfrac{2\left(x+2\right)}{x-4}=\dfrac{2x+4}{x-4}\)


a. Em tự giải
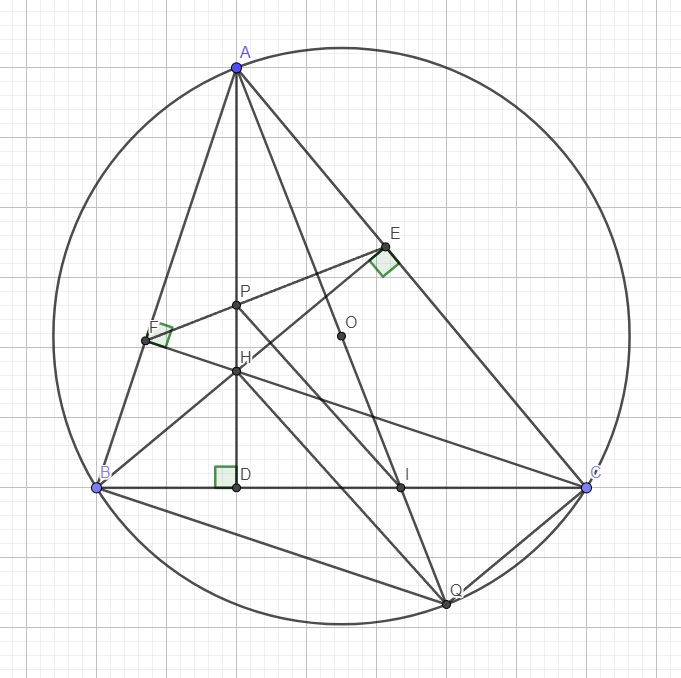
b.
Ta có: \(\widehat{ABC}=\widehat{AQC}\) (cùng chắn AC) (1)
Do AQ là đường kính \(\Rightarrow\widehat{ACQ}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{ACQ}=90^0\) \(\Rightarrow\widehat{ACQ}+\widehat{CAQ}=90^0\) (2)
Tam giác ABD vuông tại D \(\Rightarrow\widehat{BAD}+\widehat{ABC}=90^0\) (3)
(1);(2);(3) \(\Rightarrow\widehat{CAQ}=\widehat{BAD}\)
c.
\(\left\{{}\begin{matrix}\widehat{PAE}=\widehat{PAI}+\widehat{CAQ}\\\widehat{IAB}=\widehat{PAI}+\widehat{BAD}\\\widehat{CAQ}=\widehat{BAD}\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow\widehat{PAE}=\widehat{IAB}\) (3)
Tứ giác BCEF nội tiếp (E và F cùng nhìn BC dưới 1 góc vuông)
\(\Rightarrow\widehat{ABI}+\widehat{CEF}=180^0\)
Mà \(\widehat{CEF}+\widehat{AEP}=180^0\)
\(\Rightarrow\widehat{AEP}=\widehat{ABI}\) (4)
(3);(4) \(\Rightarrow\Delta AEP\sim\Delta ABI\left(g.g\right)\)
\(\Rightarrow\dfrac{AP}{AI}=\dfrac{AE}{AB}\) (5)
AQ là đường kính \(\Rightarrow\widehat{ABQ}\) là góc nt chắn nửa đường tròn \(\Rightarrow\widehat{ABQ}=90^0\)
Xét 2 tam giác ABQ và AEH có: \(\left\{{}\begin{matrix}\widehat{ABQ}=\widehat{AEH}=90^0\\\widehat{BAQ}=\widehat{EAH}\left(\text{theo (3)}\right)\end{matrix}\right.\) \(\Rightarrow\Delta ABQ\sim\Delta AEH\left(g.g\right)\)
\(\Rightarrow\dfrac{AE}{AB}=\dfrac{AH}{AQ}\) (6)
(5);(6) \(\Rightarrow\dfrac{AH}{AQ}=\dfrac{AP}{AI}\) \(\Rightarrow\dfrac{AP}{AH}=\dfrac{AI}{AQ}\)
\(\Rightarrow PI||HQ\) (định lý Talet đảo)
 so sánh ạaa
so sánh ạaa rút gọn ạaa
rút gọn ạaa
 giúp e với ạaa
giúp e với ạaa

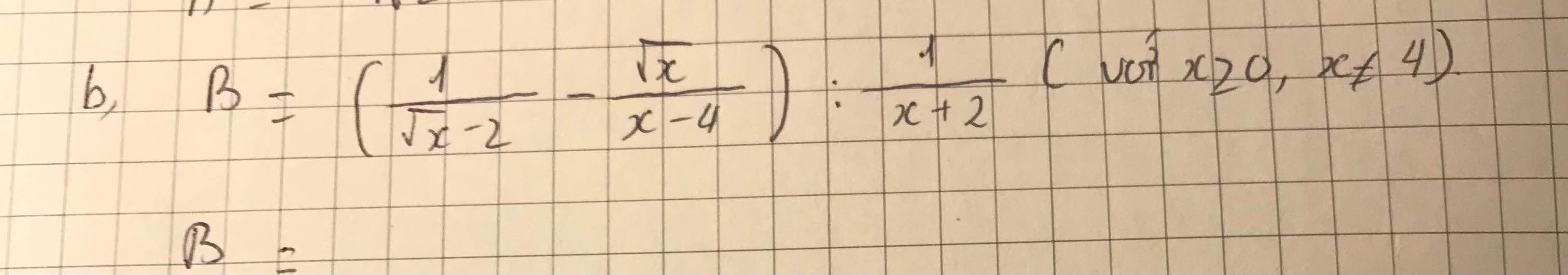
 giúp e với ạaa
giúp e với ạaa
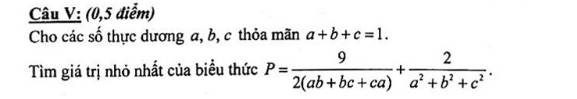 giúp e vs ạaa
giúp e vs ạaa
(2-căn 2)^2=6-4*căn 2=1/4+23/4-4căn 2
(1/2)^2=1/4
mà 23/4-4căn 2>0
nên 2-căn 2>1/2