
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

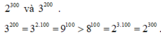

ta có :
2300=(23)100=8100
3200=(32)100=9100
vì 8100<9100 nên 2300<3200
\(2^{300}=\left(2^3\right)^{100}\) \(\Rightarrow8^{100}\)
\(3^{200}=\left(3^2\right)^{100}\) \(\Rightarrow9^{100}\)
\(\Rightarrow8^{100}<9^{100}\)\(\Leftrightarrow2^{300}<3^{200}\)


Ta có: \(2^{300}=2^{3^{100}}=8^{100}\)
\(3^{200}=3^{2^{100}}=9^{100}\)
Mà \(8^{100}<9^{100}\)
=> \(2^{300}<3^{200}\)


Bài 1:
a: Sửa đề: 1/3^200
1/2^300=(1/8)^100
1/3^200=(1/9)^100
mà 1/8>1/9
nên 1/2^300>1/3^200
b: 1/5^199>1/5^200=1/25^100
1/3^300=1/27^100
mà 25^100<27^100
nên 1/5^199>1/3^300

2^300 = (2³)^100 = 8^100
3^200 = (3²)^100 = 9^100
Vì 8 < 9 nên 8^100 < 9^100 =>2^300 < 3^200.
\(2^{300}=2^{3\times100}=\left(2^3\right)^{100}=8^{100}\)
\(3^{200}=3^{2\times100}=\left(3^2\right)^{100}=9^{100}\)
vì 8^100< 9^100 nên 2^300<3^200

Ta có :
\(.2^{300}=2^{3.100}=\left(2^3\right)^{100}=8^{100}\)
\(3^{200}=3^{2.100}=\left(3^2\right)^{100}=9^{100}\)
Ta lại có : 8<9
=> 8100<9100
=> 2300<3200
2300=\(\left(2^3\right)^{100}=8^{100}\)
\(3^{200}=\left(3^2\right)^{100}=9^{100}\)
vì \(8^{100}< 9^{100}\Rightarrow2^{300}< 3^{200}\)

\(2^{300}=\left(2^3\right)^{100}=8^{100}< 9^{100}=\left(3^2\right)^{100}=3^{200}\)

`a)2^{300}=(2^3)^100=8^100`
`3^200=(3^2)^100=9^100`
Vì `9^100>8^100`
`=>2^300<3^200`
`b)3xx24^10`
`=3.(3.8)^10`
`=3^{11}.8^10`
`=3^{11}.2^30`
`2^300=2^{30}.2^{270}`
`=2^{30}.8^{90}`
Vì `3^11<8^90`
`=>3^{11}.2^30<8^{90}.2^30=2^300`
`=>3xx24^{10}<2^300+3^20+4^30`