Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)
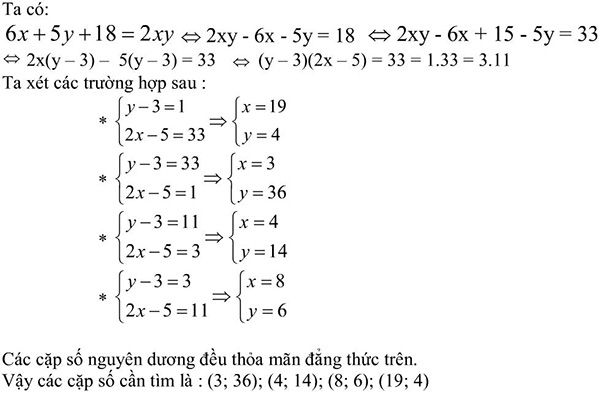
b)
Nhận thấy: x phải là số lẻ. Vì nếu x là số chẵn thì 3x^2 sẽ là số chẵn => 3x^2-4y^2 là số chẵn trong khi 13 là số lẻ
x là số lẻ => x có dạng x= 2k+1 với k thuộc Z
thay x=2k+1 vào phương trình ta có:
3(4k^2+4k+1) - 4y^2 = 13
<=> 6k^2+6k-2y^2=5
<=> 6k(k+1) = 5+2y^2
Dễ thấy vế trái là số chẵn trong khi vế phải là số lẻ => phương trình không có nghiệm nguyên => dpcm

Ta có A = (x + y)(x + 2y)(x + 3y)(x + 4y) + y4
= (x2 + 5xy + 4y2)( x2 + 5xy + 6y2) + y4
Đặt x2 + 5xy + 5y2 = t ( t Z) thì
A = (t - y2)( t + y2) + y4 = t2 –y4 + y4 = t2 = (x2 + 5xy + 5y2)2
V ì x, y, z Z nên x2 Z, 5xy Z, 5y2 Z x2 + 5xy + 5y2 Z
Vậy A là số chính phương.

Bài 1: Chứng minh rằng mọi số nguyên x, y thì:
A = (x + y)(x + 2y)(x + 3y)(x + 4y) + là số chính phương.
Giải: Ta có A = (x + y)(x + 2y)(x + 3y)(x + 4y) + y4
= (x2 + 5xy + 4y2)(x2 + 5xy + 6y2) + y4
Đặt x2 + 5xy + 5y2 = t (t ∈ Z) thì
A = (t - y2)(t + y2) + y4 = t2 - y4 + y4 = t2 = (x2 + 5xy + 5y2)2
Vì x, y, z ∈ Z nên x2 ∈ Z, 5xy ∈ Z, 5y2 ∈ Z => (x2 + 5xy + 5y2) ∈ Z
Vậy A là số chính phương.
Bài 2: Chứng minh tích của 4 số tự nhiên liên tiếp cộng 1 luôn là số chính phương.
Giải: Gọi 4 số tự nhiên, liên tiếp đó là n, n + 1, n + 2, n + 3 (n ∈ Z). Ta có:
n(n + 1)(n + 2)(n + 3) + 1 = n . ( n + 3)(n + 1)(n + 2) + 1
= (n2 + 3n)(n2 + 3n + 2) + 1 (*)
Đặt n2 + 3n = t (t ∈ N) thì (*) = t(t + 2) + 1 = t2 + 2t + 1 = (t + 1)2
= (n2 + 3n + 1)2
Vì n ∈ N nên n2 + 3n + 1 ∈ N. Vậy n(n + 1)(n + 2)(+ 3) + 1 là số chính phương.

\(\frac{3x}{4}=\frac{2y}{5}\Leftrightarrow15x=8y\Leftrightarrow7,5x=4y\)
Mà \(9x-4y=32\)
nên \(9x-7,5x=32\Leftrightarrow1,5x=32\Leftrightarrow x=\frac{64}{3}\Rightarrow y=40\)
3x/4=2y/5 =>9x/12=4y/10
Áp dụng tính chất dãy tỉ số bằng nhau ta có
9x/12=4y/10=9x-4y/12-10=32/2=16
3x/4=16=>x=16.4:3=64/3
2y/5=16=>y=16.5;2=40