
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


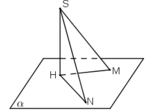
Giả sử ta có hai đường xiên SM, SN và các hình chiếu HM, HN của chúng trên mp (α).
Vì SH ⊥ mp(α)
⇒ SH ⊥ HM và SH ⊥ HN
⇒ ΔSHN và ΔSHM vuông tại H.
Áp dụng định lí Py-ta- go vào hai tam giác vuông này ta có:
⇒ S M 2 = S H 2 + H M 2 ; v à S N 2 = S H 2 + H N 2 . a ) S M = S N ⇔ S M 2 = S N 2 ⇔ H M 2 = H N 2 ⇔ H M = H N . b ) S M > S N ⇔ S M 2 > S N 2 ⇔ H M 2 > H N 2 ⇔ H M > H N .

Gọi số cần tìm là \(\overline{abcd}\Rightarrow a>b>c>d\)
Với mỗi bộ 4 chữ số phân biệt lập ra từ \(\left\{0;1;2;...;9\right\}\) luôn có duy nhất 1 cách sắp xếp thỏa mãn yêu cầu bài toán
\(\Rightarrow\) Có \(C_{10}^4=210\) số thỏa mãn yêu cầu
//Ps: do a lớn nhất nên cứ yên tâm rằng ko bao giờ rơi vào trường hợp số 0 đứng đầu cả, chừng nào bài toán cho \(a< b< c< d\) lúc đó mới cần xét a

a) Khoảng cách từ un tới 0 trở nên rất nhỏ (gần bằng 0) khi n trở nên rất lớn
b) Bắt đầu từ số hạng u100 của dãy số thì khoảng cách từ un đến 0 nhỏ hơn 0,01
Bắt đầu từ số hạng u1000 của dãy số thì khoảng cách từ un đến 0 nhỏ hơn 0,001

a) Giả sử ta có hai đường xiên SA, SB và các hình chiếu HA, HB của chúng trên mp(α)
Giả sử HA = HB
Vì SH ⊥ mp(α) nên SH ⊥ HA và SH ⊥ SB và các tam giác SHA, SHB là các tam giác vuông. Hai tam giác vuông SHA, SHB có canh SH chung và HA = HB nên :
ΔSHA = ΔSHB SA = SB
Ngược lại nếu SA = SB thì ΔSHA = ΔSHB ⇒ HA = HB
Kết quả, ta có HA = HB SA= SB (đpcm)
b) Giả sử có hai đường xiên SA, SC và các hình chiếu HA, HC của chúng trên mp(α) với giả thiết HC > HA.
Trên đoạn HC, lấy điểm B' sao cho HA' = HA ⇒ HC > HA'. Như vậy, theo kết quả câu a) ta có SA' = SA. Ta có trong các tam giác vuông SHB', SHC thì :
SC2= SH2 + HC2
SA2 = SH2 + HA2
Vì HC > HA' nên SC2 > SA2 ⇒ SC > SA
Suy ra SC > SA
Như vậy HC > HA ⇒ SC > SA
Lí luận tương tự, ta có : SC > SA ⇒ HC > HA
Kết quả : HC > HA ⇔ SC > SA
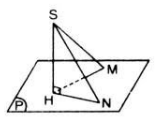
a) Gọi SN là một đường xiên khác. Xét hai tam giác vuông SHM và SHN có SH chung. Nếu SM = SN => tam giác SHM = tam giác SHN => HM = HN, ngược lại nếu HM = HN thì tam giác SHM = tam giác SHNSM => SM = SN.
b) Xét tam giác vuông SHM và SHN có SH chung. Nếu SN > SM thì \(HN^2-SN^2-SH^2\) => \(SM^2-SH^2=HM^2\) => HN > HM. Chứng minh tương tự cho chiều ngược lại.

Đáp án C.
Số cách chọn ngẫu nhiên 2 lá phiếu là: C 9 2 = 36 (cách)
Các cặp số có tổng là một số lẻ lớn hơn hoặc bằng 15 là: (9;8); (9;6); (8;7). Xác suất để tổng của hai số ghi trên hai lá phiếu rút được là một số lẻ lớn hơn hoặc bằng 15 là: 3 36 = 1 12

Đáp án C
Số cách rút hai lá phiếu là C 9 2
Gọi p là biến cố hai lá phiếu rút được có tổng lẻ lớn hơn hoặc bằng 15
![]()
![]()

Lời giải:
Gọi số đầu tiên trong csn trên là $u_1$ và công bội là $q$
$u_1-u_2=35$
$\Leftrightarrow u_1-u_1q=35$
$\Leftrightarrow u_1(1-q)=35(1)$
$u_3-u_4=560$
$\Leftrightarrow u_1q^2-u_1q^3=560$
$\Leftrightarrow u_1q^2(1-q)=560(2)$
Từ $(1); (2)\Rightarrow q^2=560:35=16$
$\Rightarrow q=\pm 4$
Nếu $q=4$ thì $u_1=\frac{-35}{3}$
$u_2=\frac{-35}{3}.4=\frac{-140}{3}; u_3=\frac{-140}{3}.4=\frac{-560}{3}; u_4=\frac{-2240}{3}$
Tương tự với $q=-4$

EM CHƯA HỌC 11
oo+1 nha