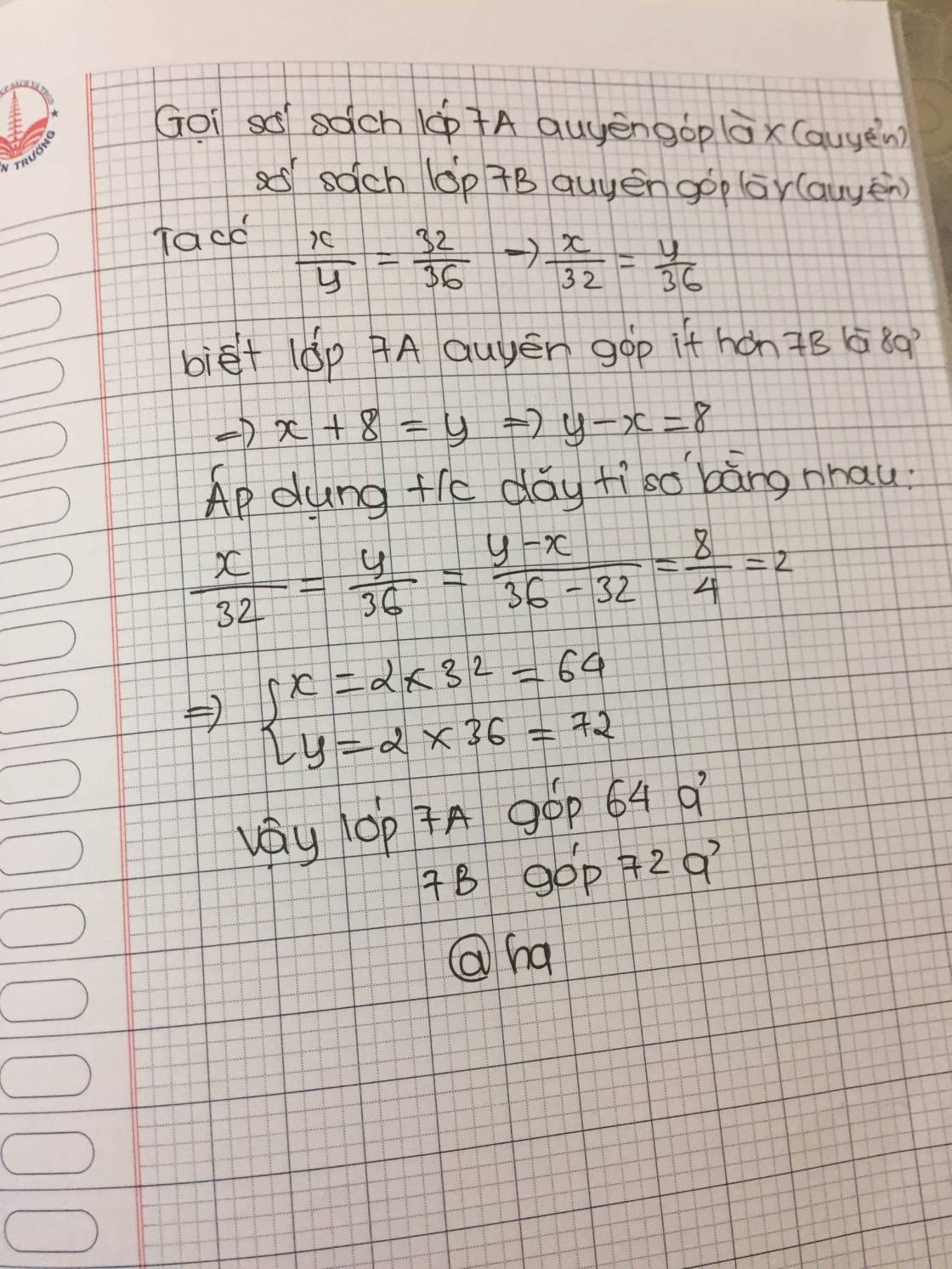Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{4a-b-c}{4\cdot2-3-4}=\dfrac{20}{1}=20\)
Do đó: a=40; b=60; c=80

Mỗi học sinh quyên góp được :
\(8:\left(36-32\right)=2\left(q\right)\)
Số sách lớp 7A quyên góp được :
\(32.2=64\left(q\right)\)
Số sách lớp 7B quyên góp được :
\(36.2=72\left(q\right)\)

Gọi số giấy 3 lớp là a,b,ca,b,c
Theo đề bài: a/3 = b/6 = c/7 và 2b−(a+c)=150
→ a/3 = 2b/12 = c/7
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
a/3 = 2b/12 = c/7 = 2b−(a+c)/12−(3+7) = 150/2 = 75
→ a/3 = 75 → a = 75.3 = 225
→ b/6 = 75 → b = 75.6 = 450
→ c/7 = 75 → c = 75.7 = 525
Vậy a, b, c lần lượt =.......................

Gọi số quyển sách 2 lớp 7A và 7B quyên góp được lần lượt là a,b (quyển) (a,b \(\in N\))
Vì số sách của lớp 7A và 7B tỉ lệ thuận với số học sinh 2 lớp lần lượt là 32 và 36 nên ta có :
\( \Rightarrow \dfrac{{a}}{{32}} = \dfrac{{b}}{{36}}\)
Theo đề bài số sách lớp 7A ít hơn 7B 8 quyển nên ta có : b – a = 8 (quyển sách)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\( \dfrac{{a}}{{32}} = \dfrac{{b}}{{36}} \Rightarrow \dfrac{{b - a}}{{36 - 32}} = \dfrac{8}{4} = 2\)
Xét \(\dfrac{{a}}{{32}} = 2 \Rightarrow a = 32.2\) \( \Rightarrow a = 64\)(quyển sách)
Vậy số sách lớp 7A quyên góp được là: 64 quyển sách
Số sách lớp 7B = 64 + 8 = 72 (quyển sách)

Gọi khối lượng giấy vụn lớp 9A,9B,9C quyên góp được lần lượt là a,b,c
Theo đề, ta có: a/3=b/4=c/5 và a+b+c=240
Áp dụng tính chât củaDTSBN, ta được:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{3+4+5}=\dfrac{240}{12}=20\)
=>a=60; b=80; c=100
Gọi \(x,y,z\) lần lượt là số kg giấy vụn mà 3 lớp 9A,9B,9C quyên góp được \(\left(x,y,z\in N\right)\)
Vì số kg giấy vụn quyên góp được của mỗi lớp lần lượt tỉ lệ với 3:4:5
\(\Rightarrow\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}\)
Vì ba lớp 9A,9B,9C quyên góp được 240 kg giấy vụn
\(\Rightarrow x+y+z=240\)
Áp dụng tính chất của dãy tỉ số bằng nhau :
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{x+y+z}{3+4+5}=\dfrac{240}{12}=20\)
\(+)\)\(\dfrac{x}{3}=20\Rightarrow x=20\times3=60\)
\(+)\)\(\dfrac{y}{4}=20\Rightarrow y=20\times4=80\)
\(+)\)\(\dfrac{z}{5}=20\Rightarrow z=20\times5=100\)
Vậy \(60,80,100\) lần lượt là số kg giấy vụn mà 3 lớp 9A,9B,9C quyên góp được

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{5}=\dfrac{b}{7}=\dfrac{b-a}{7-5}=\dfrac{14}{2}=7\)
Do đó: a=35; b=49

Gọi số sách lớp 7A,7B góp vào lần lượt là a,b (quyển) (a,b:nguyên, dương)
Ta được:
\(\dfrac{a}{5}=\dfrac{b}{7}=\dfrac{b-a}{7-5}=\dfrac{14}{2}=7\\ \Rightarrow a=7.5=35\left(quy\text{ển}\right);b=7.7=49\left(quy\text{ển}\right)\)
Vậy lớp 7A góp vào 35 quyển, lớp 7B góp vào 49 quyển

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{12}=\dfrac{b}{14}=\dfrac{c}{13}=\dfrac{b-c}{14-13}=33\)
Do đó: a=396; b=462; c=429

Gọi số tập mà các bạn của ba lớp 7A, 7B và 7C tham gia quyên góp lần lượt là a(quyển),b(quyển),c(quyển)(Điều kiện: a,b,c∈Z+)
Vì số quyển tập quyên góp được của 3 lớp 7A, 7B và 7C lần lượt tỉ lệ với 36;42 và 39
nên a:b:c=36:42:39
hay \(\dfrac{a}{36}=\dfrac{b}{42}=\dfrac{c}{39}\)
Vì số quyển tập lớp 7C quyên góp ít hơn lớp 7B 33 quyển nên b-c=33
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{36}=\dfrac{b}{42}=\dfrac{c}{39}=\dfrac{b-c}{42-39}=\dfrac{33}{3}=11\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{a}{36}=11\\\dfrac{b}{42}=11\\\dfrac{c}{39}=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=396\left(nhận\right)\\b=462\left(nhận\right)\\c=429\left(nhận\right)\end{matrix}\right.\)
Vậy: Lớp 7A quyên góp 396 quyển tập
Lớp 7B quyên góp 462 quyển tập
Lớp 7C quyên góp 429 quyển tập
Gọi số tập mà các bạn của ba lớp 7A, 7B và 7C tham gia quyên góp lần lượt là a(quyển),b(quyển),c(quyển)(Điều kiện: a,b,c∈Z+)
Vì số quyển tập quyên góp được của 3 lớp 7A, 7B và 7C lần lượt tỉ lệ với 36;42 và 39
nên a:b:c=36:42:39
hay a36=b42=c39a36=b42=c39
Vì số quyển tập lớp 7C quyên góp ít hơn lớp 7B 33 quyển nên b-