Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta thấy: Lớp 8C có 40 học sinh nhưng bảng thống kê lại có 41 học sinh dự thi. Vậy dữ liệu số học sinh dự thi của lớp 8C là dữ liệu không hợp lí.

a)
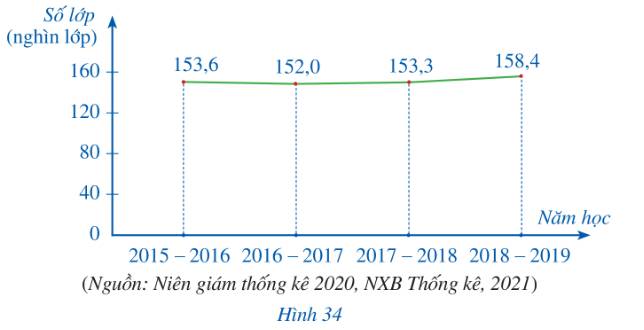
Năm học | 2015 - 2016 | 2016 - 2017 | 2017 - 2018 | 2018 - 2019 |
Số lớp học ở cấp THCS (nghìn lớp) | 153,6 | 152,0 | 153,3 | 158,4 |
b) Tỉ số phần trăm giữa số lớp học cấp THCS ở Việt Nam năm học 2018 – 2019 với năm học 2015 – 2016 là:
\(\frac{{158,4.100}}{{153,6}}\% = 103,125\% \)
So với năm học 2015 – 2016, số lượng lớp học ở cấp THCS của Việt Nam trong năm học 2018 – 2019 đã tăng lên số phần trăm là:
\(103,125 - 100 = 3,1\% \)
c) Có một số giải pháp để tăng số lượng lớp học ở cấp THCS ở Việt Nam trong những năm học tới là:
- Đẩy mạnh việc đào tạo đội ngũ giáo viên.
- Tăng cường cơ sở vật chất cho các trường học hiện có.
- Xây thêm các trường học mới.

a) Quan sát bảng trên ta thấy khi x = 1; x = 2; x = 3; x = 4; x = 5; x = 6 thì ta đều xác định giá trị của y là y = − 2.
Vì với mỗi giá trị của x ta xác định được một giá trị của y nên đại lượng y là hàm số của đại lượng x.
b) Quan sát bảng trên ta thấy khi x = 1; x = 2; x = 3; x = 4; x = 1; x = 5 thì ta đều xác định giá trị của y lần lượt là: y = − 2; y = − 3; y = − 4; y = − 5; y = − 6; y = − 7.
Vì x = 1 nhận hai giá trị y = -2 và y = -6 nên đại lượng y không là hàm số của đại lượng x.



Nên sử dụng biểu đồ cột.
Vì ƯCLN(13,46,183) = 1 nên nếu dùng biểu đồ tranh sẽ phải vẽ rất nhiều biểu tượng (13 + 47 + 183 = 243 (biểu tượng))