Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: -10/8<-1
-19/19=-1
-1<-2/10<0
0<5/12<1<17/15
=>17/15>1>5/12>-2/10>-19/19>-10/8
b: -1/3=-4/12; -5/12=-5/12; -3/4=-9/12; -1/4=-3/12; -7/12=-7/12
=>-3/4<-7/12<-5/12<-1/3<-1/4

Ta có:
\(-\frac{2}{3} = -0,\left( 6 \right);\,\,\,\,\,4,1;\,\,\, - \sqrt 2 = - 1,414...;\,\,\,\,3,2;\\\pi = 3,141...;\,\,\,\, - \frac{3}{4} = - 0,75;\,\,\,\,\frac{7}{3} = 2,\left( 3 \right)\).
Do \( - 1,414... < - 0,75 < -0,\left( 6 \right) < 2,\left( 3 \right) < 3,141... < 3,2 < 4,1\)
Nên \( - \sqrt 2 < - \frac{3}{4} < -\frac{2}{3} < \frac{7}{3} < \pi < 3,2 < 4,1.\)

Thứ tự từ nhỏ đến lớn:\(\frac{-5}{2};-1,5;-1.34;-50\%;0;1;6,7\)

a: \(-3< -2.15< -\sqrt{3}< 0< \dfrac{13}{7}< \sqrt{8}< \dfrac{33}{12}\)
b: \(0< \sqrt{3}< \dfrac{13}{7}< 2.15< \dfrac{33}{12}< \sqrt{8}< 3\)

Đổi : \(\dfrac{-1}{2}\)
= -0,5
Ta có :
a) Theo thứ tự từ nhỏ đến lớn : -3,2 ; -1,5 ; -0,5 ; 0 ; 1 ; 7,4 .
b) l -3,2 l = 3,2 l 1 l = 1
l -0,5 l = 0,5 l 7,4 l = 7,4
l 0 l = 0 l -1,5 l = 1,5
Thro thứ tự từ nhỏ đến lớn của các giá trị tuyệt đối của chúng : 0 ; 0,5 ; 1 ; 1,5 ; 3,2 ; 7,4 .
Chúc bạn học tốt !
a) Theo thứ tự từ nhỏ đến lớn: -3,2; -1,5; \(\dfrac{-1}{2}\); 0; 1; 7,4.
b) Theo thứ tự từ nhỏ đến lớn của các giá trị tuyệt đối của chúng: 0; \(\dfrac{-1}{2}\) ; 1; -1,5; -3,2; 7,4.

x=2^100 suy ra x=16^25
y=3^75 suy ra y= 27^25
z=5^50 suy ra z= 25^25
Ta thấy: 16^25<25^25<27^25
Suy ra x<z<y
Sắp xếp: x,z,y
k mình nhaa!!! Mơn bạn nhìu
x=2^100 suy ra x=16^25
y=3^75 suy ra y= 27^25
z=5^50 suy ra z= 25^25
Ta thấy: 16^25<25^25<27^25
Suy ra x<z<y
Sắp xếp: x,z,y

Giải :
-3 = -3
2 = 2
2,13 = 2,13
-√2 = -1,414
\(\frac{3}{7}\)= 0,428
⇒ -3 < -√2 < \(\frac{3}{7}\) < 2 < 2,13
CHÚC BẠN HỌC TỐT ^_^
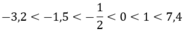
có \(-\dfrac{2}{3}=0,\left(6\right)\)
\(-\sqrt{7}\approx-2,6\)
Thứ tự từ bé đến lớn là :
\(-10;-\sqrt{7};-\dfrac{2}{3};4,1;12,\left(1\right)\)
Ta có:
\(10=\sqrt{100}>\sqrt{7}>\sqrt{4}=2\)
=> \(-\sqrt{10}< -\sqrt{7}< -2\)
------------------------
\(0< \dfrac{2}{3}< 1\)
=> \(0>-\dfrac{2}{3}>-1\)
=> \(-10< -\sqrt{7}< -\dfrac{2}{3}\)
Lại có: `0 < 4,1 < 12,(1)`
Nên thứ tự cần sắp xếp là:
\(-10< -\sqrt{7}< -\dfrac{2}{3}< 4,1< 12,\left(1\right)\)