Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a) thứ tự từ lớn đến bé là : 3/5;3/6;3/7
b)thứ tự từ bé đến lớn là :1/2; 2/4; 1;5/2;8/2
Bài 2:
a)7/8<8/9
b)4/6<7/8

a) 3/8<3/4<5/6<8/6 b) 3/8<3/4<5/6<8/6 c)3/8<3/4<5/6<8/6 d)3/8<3/4<5/6<8/6
xếp các phân số 3/2 , 2/8 , 5/16 , 3/4 theo thứ tự từ bé đến lớn

Ta có: \(\frac{5}{5}=1\)
Ta thấy \(\frac{3}{4}\)và \(\frac{4}{5}\)đều nhỏ hơn 1. Ta quy đồng \(\frac{3}{4}\)và \(\frac{4}{5}\):
\(\hept{\begin{cases}\frac{3}{4}=\frac{15}{20}\\\frac{4}{5}=\frac{16}{20}\end{cases}}\)
Mà \(\frac{15}{20}< \frac{16}{20}\Rightarrow\frac{3}{4}< \frac{4}{5}< 1\) Hay \(\frac{3}{4}< \frac{4}{5}< \frac{5}{5}\)(1)
Ta thấy \(\frac{7}{6}\)và \(\frac{8}{7}\)đều lớn hơn 1. Ta quy đồng \(\frac{7}{6}\)và \(\frac{8}{7}\):
\(\hept{\begin{cases}\frac{7}{6}=\frac{49}{42}\\\frac{8}{7}=\frac{48}{42}\end{cases}}\)
Mà \(\frac{48}{42}< \frac{49}{42}\Rightarrow\frac{8}{7}< \frac{7}{6}\Rightarrow1< \frac{8}{7}< \frac{7}{6}\)Hay \(\frac{5}{5}< \frac{8}{7}< \frac{7}{6}\)(2)
Từ (1) và (2) ta có thứ tự sau: \(\frac{3}{4}< \frac{4}{5}< \frac{5}{5}< \frac{8}{7}< \frac{7}{6}\)
\(\)
ta so sánh với 1 thì thấy :
3/4 và 4/5 < 1 ; 5/5 = 1 ; 7/6 và 8/7 > 1
ta so sánh 3/4 và 4/5 bằng cách quy đồng mẫu số
3/4 = 15/20 ; 4/5 = 16/20
vậy 3/4 < 4/5 vì 15/2<16/20
tiếp theo ta thấy 7/6 và 8/7 > 1 nên so sánh hai phân số 7/6 và 8/7
ta quy đồng mẫu số
7/6 = 49/42 ; 8/7 = 48/42
vậy 7/6 > 8/7 vì 49/42>48/42
vậy kết quả là
3/4 ; 4/5;5/5 ; 7/6 ; 8/7

Mình làm mẫu 1 câu thôi nha
a) Quy đồng tất cả, mẫu chung là 24 (Cái này tự quy đồng)
=> 5/6 = 20/24 ; 3/8 = 9/24 ; 3/4 = 18/24 ; 8/6 = 32/24
Sắp xếp theo thứ tự từ bé -> lớn là: 9/24 ; 18/24 ; 20/24 ; 32/24
Vậy ta có: 3/8 ; 3/4 ; 5/6 ; 8/6

\(\frac{4}{5};\frac{6}{7};\frac{3}{4};\frac{8}{9};1;\frac{7}{8};\frac{5}{6}\)
=> Thứ tự từ lớn đến bé là :
\(1;\frac{8}{9};\frac{7}{8};\frac{6}{7};\frac{5}{6};\frac{4}{5};\frac{3}{4}\)
Học tốt ~

Bài 1:
\(\frac{1}{12},\frac{2}{3},\frac{3}{4},\frac{5}{6}\)
Bài 2:
A. \(\frac{11}{6}\)
B. \(\frac{3}{32}\)
C. \(\frac{1}{7}\)
D. \(\frac{15}{8}\)
Tích đúng cho mình nhé!
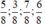
Đáp án là D