Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(\dfrac{-5}{6}=\dfrac{-20}{24};\dfrac{7}{8}=\dfrac{21}{24};\dfrac{7}{24}=\dfrac{7}{24};\dfrac{-3}{4}=-\dfrac{18}{24};\dfrac{2}{3}=\dfrac{16}{24}\)
Do đó: \(\dfrac{-5}{6}< -\dfrac{3}{4}< \dfrac{7}{24}< \dfrac{2}{3}< \dfrac{7}{8}\)
\(\dfrac{7}{8}=\dfrac{119}{136};\dfrac{16}{17}=\dfrac{128}{136}\)
mà 119<128
nên 7/8<16/17
DO đó: -5/6<-3/4<7/24<2/3<7/8<16/17
b: \(\dfrac{-5}{8}=\dfrac{-95}{8\cdot19};\dfrac{-16}{19}=\dfrac{-128}{19\cdot8}\)
Do đó: -5/8>-16/19
\(\dfrac{7}{10}=0.7;\dfrac{20}{23}\simeq0.87;\dfrac{214}{315}\simeq0.68;\dfrac{205}{107}>1\)
Do đó: \(\dfrac{205}{107}>\dfrac{20}{23}>\dfrac{7}{10}>\dfrac{214}{315}>-\dfrac{5}{8}>-\dfrac{16}{19}\)

a) \(\dfrac{-5}{6}=\dfrac{-340}{408}\);\(\dfrac{7}{8}=\dfrac{357}{408}\);\(\dfrac{7}{24}=\dfrac{119}{408}\)
\(\dfrac{16}{17}=\dfrac{384}{408}\); \(\dfrac{-3}{4}=\dfrac{-306}{408}\); \(\dfrac{2}{3}=\dfrac{272}{408}\)
Do đó: \(\dfrac{-5}{6}< \dfrac{-3}{4}< \dfrac{7}{24}< \dfrac{2}{3}< \dfrac{7}{8}< \dfrac{16}{17}\)

\(\dfrac{-1}{2}=\dfrac{-9}{18};\dfrac{-5}{9}=\dfrac{-10}{18};\dfrac{-1}{3}=\dfrac{-6}{18}\)
mà -10<-9<-6<0
nên \(-\dfrac{5}{9}< -\dfrac{1}{2}< -\dfrac{1}{3}< 0\)(1)
Ta có: \(\dfrac{5}{12}=\dfrac{15}{36};\dfrac{7}{18}=\dfrac{14}{36};\dfrac{1}{3}=\dfrac{12}{36}\)
mà \(0< \dfrac{12}{36}< \dfrac{14}{36}< \dfrac{15}{36}\)
nên \(0< \dfrac{1}{3}< \dfrac{7}{18}< \dfrac{5}{12}\left(2\right)\)
Từ (1),(2) suy ra \(-\dfrac{5}{9}< -\dfrac{1}{2}< -\dfrac{1}{3}< \dfrac{1}{3}< \dfrac{7}{18}< \dfrac{5}{12}\)

1) \(\dfrac{3}{2}\) : \(\dfrac{9}{4}\) =\(\dfrac{3}{2}\)x\(\dfrac{4}{9}\)=\(\dfrac{12}{18}\)=\(\dfrac{2}{3}\)
2)\(\dfrac{48}{55}\) : \(\dfrac{12}{11}\)= \(\dfrac{48}{55}\) x\(\dfrac{11}{12}\)= \(\)\(\dfrac{528}{660}\)=\(\dfrac{4}{5}\)
3)\(\dfrac{7}{10}\) : \(\dfrac{7}{5}\)=\(\dfrac{7}{10}\) x \(\dfrac{5}{7}\)= \(\dfrac{35}{70}\)=\(\dfrac{1}{2}\)
4)\(\dfrac{6}{7}\) : \(\dfrac{8}{7}\) = \(\dfrac{6}{7}\) x \(\dfrac{7}{8}\) =\(\dfrac{42}{56}\)=\(\dfrac{3}{4}\)
Sắp xếp các thương theo thứ tự tăng dần :\(\dfrac{1}{2}\);\(\dfrac{2}{3}\);\(\dfrac{3}{4}\);\(\dfrac{4}{5}\)
\(\Rightarrow\)\(\dfrac{7}{10}\) : \(\dfrac{7}{5}\) ; \(\dfrac{3}{2}\) :\(\dfrac{9}{4}\) ; \(\dfrac{6}{7}\) : \(\dfrac{8}{7}\) ; \(\dfrac{48}{55}\):\(\dfrac{12}{11}\).

a: \(\dfrac{-7}{12}=\dfrac{-7\cdot5}{12\cdot5}=\dfrac{-35}{60};\dfrac{-1}{-15}=\dfrac{1}{15}=\dfrac{4}{60};\dfrac{-5}{4}=\dfrac{-5\cdot15}{4\cdot15}=-\dfrac{75}{60}\)
\(\dfrac{3}{-5}=\dfrac{-3}{5}=\dfrac{-3\cdot12}{5\cdot12}=-\dfrac{36}{60}\)
mà -75<-36<-35<4
nên \(-\dfrac{75}{60}< -\dfrac{36}{60}< -\dfrac{35}{60}< \dfrac{4}{60}\)
=>\(\dfrac{-5}{4}< \dfrac{3}{-5}< \dfrac{-7}{12}< \dfrac{-1}{-15}\)
b: \(\dfrac{-8}{25}+\dfrac{22}{23}+\dfrac{-17}{25}\)
\(=\left(-\dfrac{8}{25}-\dfrac{17}{25}\right)+\dfrac{22}{23}\)
\(=-1+\dfrac{22}{23}=-\dfrac{1}{23}\)

a) \(\dfrac{1}{6};\dfrac{1}{3};\dfrac{1}{2};...\)
\(\Rightarrow\dfrac{1}{6};\dfrac{2}{6};\dfrac{3}{6};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{4}{6}\)
b) \(\dfrac{1}{8};\dfrac{5}{24};\dfrac{7}{24};...\)
\(\Rightarrow\dfrac{3}{24};\dfrac{5}{24};\dfrac{7}{24};...\)
Dãy có quy luật tăng dần lên 2 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{9}{24}\)
c) \(\dfrac{1}{5};\dfrac{1}{4};\dfrac{1}{3};...\)
\(\dfrac{4}{20};\dfrac{5}{20};\dfrac{6}{20};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{7}{20}\)
d) \(\dfrac{4}{15};\dfrac{3}{10};\dfrac{1}{3};...\)
\(\Rightarrow\dfrac{8}{30};\dfrac{9}{30};\dfrac{11}{30};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{12}{30}\)

\(\dfrac{3}{4}\)\(\dfrac{2}{3}\)\(\dfrac{1}{3}\)0\(\dfrac{-1}{4}\)\(\dfrac{-2}{5}\)
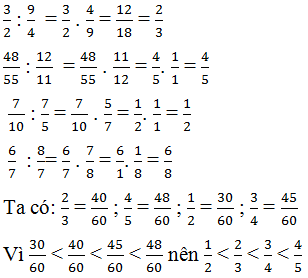
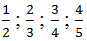


-2/3; 1/-3; 3/5; 4/5; -8/-7